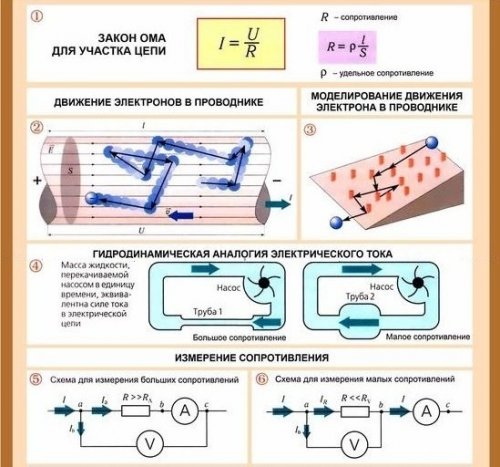
Ley de Ohm para una sección de un circuito
La ley básica de la ingeniería eléctrica que puedes usar para estudiar y calcular circuitos eléctricos es la ley de Ohm, que establece la relación entre corriente, voltaje y resistencia. Es necesario comprender claramente su esencia y poder utilizarlo correctamente en la resolución de problemas prácticos. A menudo se cometen errores en la ingeniería eléctrica debido a la incapacidad de aplicar correctamente la ley de Ohm.
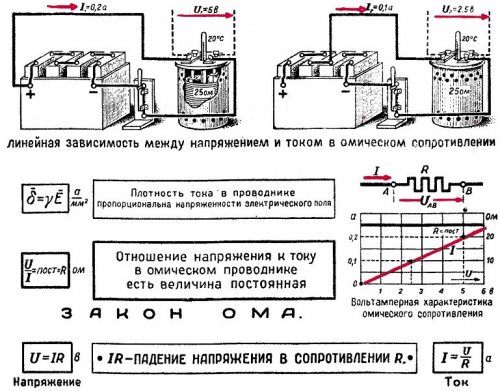
La ley de Ohm para una sección de los estados del circuito: la corriente es directamente proporcional al voltaje e inversamente proporcional a la resistencia.
Si el voltaje que actúa en un circuito eléctrico aumenta varias veces, la corriente en ese circuito aumentará en la misma cantidad. Y si aumenta la resistencia del circuito varias veces, la corriente disminuirá en la misma cantidad. Del mismo modo, el caudal de agua en la tubería es mayor cuanto mayor es la presión y menor la resistencia de la tubería al movimiento del agua.
En una forma popular, esta ley se puede formular de la siguiente manera: cuanto mayor sea el voltaje para la misma resistencia, mayor será la corriente y, al mismo tiempo, cuanto mayor sea la resistencia para el mismo voltaje, menor será el amperaje.
Para expresar matemáticamente la ley de Ohm de la forma más sencilla posible, se considera que la resistencia de un cable que lleva una corriente de 1 A a un voltaje de 1 V es de 1 Ohm.
La corriente en amperios siempre se puede determinar dividiendo el voltaje en voltios por la resistencia en ohmios. Por lo tanto, la Ley de Ohm para una sección de un circuito se escribe en la siguiente fórmula:
yo = U / R.
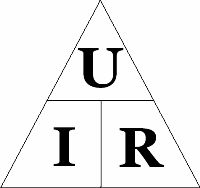
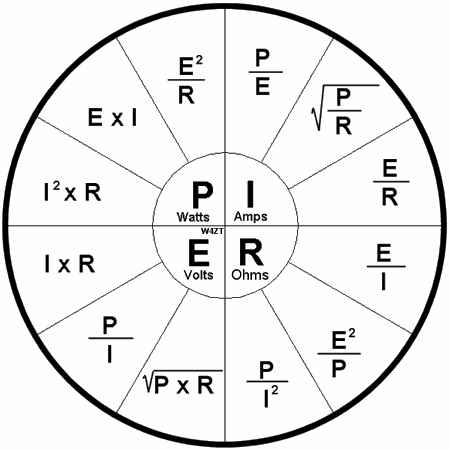
triangulo magico
Cualquier sección o elemento de un circuito eléctrico se puede caracterizar por tres características: corriente, tensión y resistencia.
Cómo usar el triángulo de Ohm: cerramos el valor requerido; otros dos símbolos darán la fórmula para su cálculo. Por cierto, solo una fórmula del triángulo se llama ley de Ohm, la que refleja la dependencia de la corriente del voltaje y la resistencia. Las otras dos fórmulas, aunque son consecuencias de ella, no tienen sentido físico.
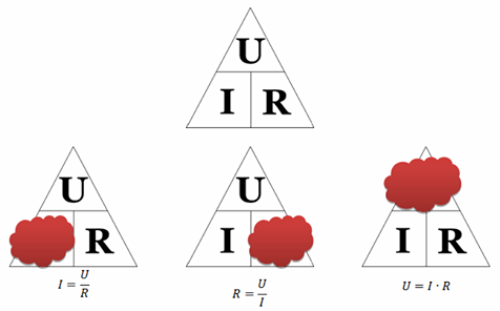
Los cálculos realizados con la ley de Ohm para una sección del circuito serán correctos cuando el voltaje esté en voltios, la resistencia esté en ohmios y la corriente esté en amperios. Si se utilizan varias unidades de estas cantidades (p. ej., miliamperios, milivoltios, megaohmios, etc.), deben convertirse a amperios, voltios y ohmios, respectivamente. Para enfatizar esto, la fórmula de la ley de Ohm para una sección de un circuito a veces se escribe de la siguiente manera:
amperio = voltio / ohmio
También puede calcular la corriente en miliamperios y microamperios, mientras que el voltaje debe expresarse en voltios y la resistencia en kilohmios y megaohmios, respectivamente.
Otros artículos sobre la electricidad de forma sencilla y económica:
Qué son el voltaje, la corriente y la resistencia: cómo se usan en la práctica
Cómo la resistencia depende de la temperatura
Fuentes de CEM y corriente: principales características y diferencias.
¿Qué es un suministro eléctrico?
Campo eléctrico y magnético: ¿cuál es la diferencia?
La ley de Ohm es válida para todas las secciones del circuito. Si es necesario determinar la corriente en una sección dada del circuito, entonces es necesario dividir el voltaje que actúa en esta sección (Fig. 1) por la resistencia de esta sección.
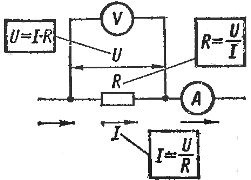
Figura 1. Aplicación de la ley de Ohm a una sección de circuito
Demos un ejemplo de cómo calcular la corriente de acuerdo con la ley de Ohm... Se requiere determinar la corriente en una lámpara con una resistencia de 2.5 ohmios, si el voltaje aplicado a la lámpara es de 5 V. Dividiendo 5 V por 2.5 ohmios, obtenemos un valor de corriente igual a 2 A. En el segundo ejemplo, determinamos la corriente que fluirá bajo la influencia de un voltaje de 500 V en un circuito cuya resistencia es de 0,5 MΩ. Para ello, expresamos la resistencia en ohmios. Dividiendo 500 V por 500 000 ohmios, encontramos la corriente en el circuito, que es 0,001 A o 1 mA.
A menudo, conociendo la corriente y la resistencia, el voltaje se determina utilizando la ley de Ohm. Escribamos la fórmula para determinar el voltaje.
U = IR
Esta fórmula muestra que el voltaje en los extremos de una sección dada del circuito es directamente proporcional a la corriente y la resistencia... El significado de esta dependencia no es difícil de entender.Si la resistencia de la sección del circuito no cambia, la corriente solo puede aumentar aumentando el voltaje. Esto significa que a una resistencia constante, una mayor corriente corresponde a un mayor voltaje. Si es necesario obtener la misma corriente con diferentes resistencias, entonces con una resistencia más alta debe haber un voltaje correspondientemente más alto.
El voltaje a través de una sección de un circuito a menudo se denomina caída de voltaje... Esto a menudo conduce a malentendidos. Mucha gente piensa que la caída de voltaje es un desperdicio de voltaje innecesario. En realidad, los conceptos de voltaje y caída de voltaje son equivalentes. Pérdidas y caídas de tensión: ¿cuál es la diferencia?
La caída de voltaje es la caída gradual en el potencial a través de un circuito que transporta corriente debido al hecho de que el circuito tiene una resistencia activa. De acuerdo con la ley de Ohm, la caída de voltaje en cada sección del circuito U es igual al producto de la resistencia de esta sección del circuito R por la corriente en ella I, es decir U-RI. Así, cuanto mayor sea la resistencia de una sección del circuito, mayor será la caída de voltaje en esa sección del circuito para una corriente dada.
El cálculo del voltaje de la ley de Ohm se puede mostrar en el siguiente ejemplo. Deje pasar una corriente de 5 mA a través de una sección del circuito con una resistencia de 10 kOhm, y es necesario determinar el voltaje en esta sección.
Al multiplicar A = 0.005 A en R — 10000 Ω, obtenemos un voltaje igual a 50 V. El mismo resultado se puede obtener al multiplicar 5 mA por 10 kΩ: U = 50 in
En los dispositivos electrónicos, la corriente suele expresarse en miliamperios y la resistencia en kiloohmios.Por lo tanto, es conveniente utilizar exactamente estas unidades de medida en los cálculos según la ley de Ohm.
La ley de Ohm también calcula la resistencia si se conocen el voltaje y la corriente. La fórmula para este caso se escribe de la siguiente manera: R = U / I.
La resistencia es siempre la relación entre el voltaje y la corriente. Si el voltaje aumenta o disminuye varias veces, la corriente aumentará o disminuirá la misma cantidad de veces. La relación voltaje-corriente igual a la resistencia permanece sin cambios.
La fórmula para determinar la resistencia no debe entenderse en el sentido de que la resistencia de un conductor dado depende de la corriente y el voltaje. Se sabe que depende de la longitud, el área de la sección transversal y el material del alambre. En apariencia, la fórmula para determinar la resistencia se asemeja a la fórmula para calcular la corriente, pero existe una diferencia fundamental entre ellas.
La corriente en una sección determinada del circuito realmente depende del voltaje y la resistencia y cambia a medida que cambian. Y la resistencia de esta sección del circuito es un valor constante que no depende de los cambios en el voltaje y la corriente, pero es igual a la relación de estos valores.
Cuando la misma corriente fluye en dos secciones del circuito y los voltajes que se les aplican son diferentes, es claro que la sección a la que se aplica el mayor voltaje tiene una resistencia correspondientemente mayor.
Y si, bajo la acción del mismo voltaje, fluye una corriente diferente en dos secciones diferentes del circuito, entonces en esta sección siempre habrá una corriente más pequeña, que tiene una mayor resistencia.Todo esto se deriva de la formulación básica de la ley de Ohm para una sección de un circuito, es decir, del hecho de que a mayor corriente, mayor voltaje y menor resistencia.
El cálculo de la resistencia usando la ley de Ohm para una sección de un circuito se mostrará en el siguiente ejemplo, se requiere encontrar la resistencia de la sección por la que fluye una corriente de 50 mA a un voltaje de 40 V. Expresando la corriente en amperios, obtenemos I = 0,05 A. Divida 40 entre 0,05 y encuentre que la resistencia es de 800 ohmios.
La ley de Ohm se puede visualizar en forma de la llamada característica corriente-voltaje... Como saben, la relación directamente proporcional entre dos cantidades es una línea recta que pasa por el origen. Esta dependencia suele llamarse lineal.
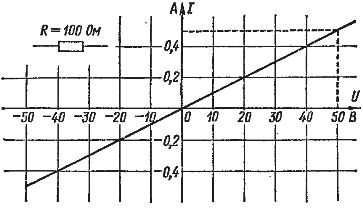
En la Fig. 2 se muestra como un gráfico de ejemplo de la ley de Ohm para una sección de circuito con una resistencia de 100 ohmios. El eje horizontal es el voltaje en voltios y el eje vertical es la corriente en amperios. La escala de corriente y voltaje se puede elegir como se desee. Se dibuja una línea recta de modo que para cada uno de sus puntos la relación voltaje/corriente sea de 100 ohmios. Por ejemplo, si U = 50 V, entonces I = 0,5 A y R = 50: 0,5 = 100 ohmios.
Arroz. 2… Ley de Ohm (Característica de corriente-voltaje)
La gráfica de la ley de Ohm para valores negativos de corriente y voltaje es la misma. Esto implica que la corriente en el circuito fluye de la misma manera en ambas direcciones. Cuanto mayor es la resistencia, menos corriente se obtiene a un voltaje dado y más cuidadosamente se mueve la línea recta.
Los dispositivos en los que la característica corriente-tensión es una línea recta que pasa por el punto de partida, es decir, la resistencia permanece constante cuando cambia la tensión o la corriente, se denominan dispositivos lineales... También se utilizan los términos circuitos lineales, resistencias lineales.
También hay dispositivos en los que la resistencia cambia cuando cambia el voltaje o la corriente. Entonces, la relación entre corriente y voltaje no se expresa de acuerdo con la ley de Ohm, sino de una manera más compleja. Para tales dispositivos, la característica de corriente-voltaje no será una línea recta que pase por el punto de partida, sino una curva o una línea discontinua. Estos dispositivos se denominan no lineales.
Ver también sobre este tema: Aplicación de la ley de Ohm en la práctica