Oscilaciones continuas y resonancia paramétrica

Vibraciones continuas: vibraciones cuya energía no cambia con el tiempo. En los sistemas físicos reales, siempre hay causas que provocan la transición de la energía vibratoria a la energía térmica (por ejemplo, la fricción en los sistemas mecánicos, la resistencia activa en los sistemas eléctricos).

Por lo tanto, solo se pueden obtener oscilaciones no amortiguadas siempre que se repongan estas pérdidas de energía. Tal reposición ocurre automáticamente en sistemas auto-oscilantes debido a la energía de una fuente externa. Las oscilaciones electromagnéticas continuas son extremadamente utilizadas. Para su obtención se utilizan diferentes generadores.

Para que las vibraciones eléctricas o mecánicas (de un círculo oscilante o de un péndulo) no estén amortiguadas, es necesario compensar las pérdidas por resistencia o fricción en todo momento.

Por ejemplo, puede actuar sobre el circuito oscilante con un EMF alterno, que aumentará periódicamente la corriente en la bobina y, en consecuencia, mantendrá la amplitud de voltaje en el capacitor.O puede empujar el péndulo de manera similar, manteniéndolo balanceándose armoniosamente.

Como saben, la magnitud de la energía del campo magnético de la bobina del circuito oscilante está relacionada con su inductancia y corriente por la siguiente relación (la segunda fórmula esenergía del campo eléctrico del capacitor mismo contorno de contorno)

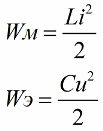
De la primera fórmula se desprende claramente que si aumentamos periódicamente la corriente en la bobina, actuando sobre el circuito EMF alterno, entonces (al aumentar o disminuir el segundo factor en la fórmula, la corriente) repondremos periódicamente este circuito con energía.

Actuando sobre el circuito estrictamente en el tiempo con sus oscilaciones libres naturales, es decir, a la frecuencia resonante, obtendremos el fenómeno de la resonancia eléctrica, porque es a la frecuencia resonante sistema oscilante absorbe más intensamente la energía que se le suministra.

Pero, ¿qué sucede si cambia periódicamente no el segundo factor (ni la corriente ni el voltaje), sino el primer factor, la inductancia o la capacitancia? En este caso, el circuito también sufrirá un cambio en su energía.

Por ejemplo, empujar periódicamente el núcleo hacia adentro y hacia afuera de la bobina o empujar hacia adentro y hacia afuera del capacitor.dieléctrico, — obtenemos también un cambio periódico muy definido en la energía del circuito.

Escribimos esta posición para un cambio de unidad en la inductancia de la bobina:

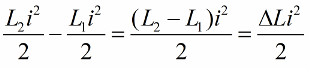
El efecto más pronunciado de la oscilación del circuito será si los cambios de inductancia se realizan justo a tiempo. Por ejemplo, si tomamos el mismo circuito en cualquier momento, cuando ya fluye una corriente i a través de él, e introducimos un núcleo en la bobina, entonces la energía cambiará en la siguiente cantidad:

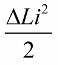
Ahora dejemos que aparezcan oscilaciones libres en el circuito mismo, pero en el momento en que, después de un cuarto de período, la energía haya pasado por completo al capacitor y la corriente en la bobina se haya vuelto cero, retiraremos abruptamente el núcleo de la bobina La inductancia volverá a su estado original, al valor inicial L. No es necesario gastar trabajo contra el campo magnético cuando se retira el núcleo. Por lo tanto, cuando el núcleo se introdujo en la bobina, el circuito recibió energía, ya que trabajamos, cuyo valor:

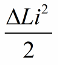
Después de una cuarta parte del período, el capacitor comienza a descargarse, su energía se convierte nuevamente en la energía del campo magnético de la bobina. Cuando el campo magnético alcance la amplitud, presionaremos el núcleo con fuerza nuevamente. Nuevamente la inductancia aumentó, aumentó en la misma cantidad.

Y nuevamente, a corriente cero, devolvemos la inductancia a su valor original. Como resultado, si las ganancias de energía para cada medio ciclo exceden las pérdidas de resistencia, la energía del bucle aumentará todo el tiempo y la amplitud de oscilación aumentará. Esta situación se expresa mediante la desigualdad:

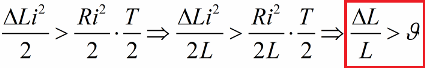
Aquí dividimos ambos lados de esta desigualdad por L y escribimos la condición de posibilidad de excitación paramétrica por saltos para un cierto valor del decremento logarítmico.

Se recomienda cambiar la inductancia (o capacitancia) dos veces por periodo, por lo que la frecuencia de cambio de parámetro (frecuencia de resonancia paramétrica) debe ser el doble de la frecuencia natural del sistema oscilante:

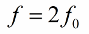
Entonces, el camino de excitación de las oscilaciones en el circuito ha aparecido sin la necesidad de cambiar directamente el EMF o la corriente.La corriente fluctuante inicial en el circuito siempre está presente de una forma u otra, y eso ni siquiera tiene en cuenta la interferencia de las oscilaciones de radiofrecuencia en la atmósfera.

Si la inductancia (o capacitancia) no cambia en saltos, sino armónicamente, entonces la condición para la aparición de oscilaciones se verá un poco diferente:

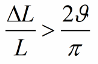
Dado que la capacitancia y la inductancia son parámetros del circuito (como la masa de un péndulo o la elasticidad de un resorte), el método de excitación de oscilaciones también se denomina excitación paramétrica.

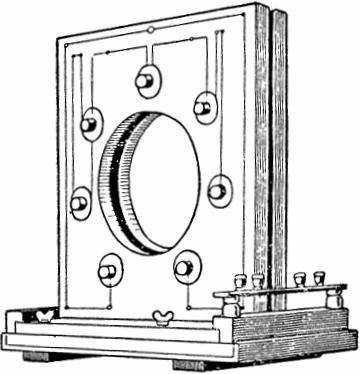
Este fenómeno fue descubierto y estudiado prácticamente a principios del siglo XX por los físicos soviéticos Mandelstam y Papalexi. En base a este fenómeno físico, construyeron el primer generador AC paramétrico con una potencia de 4 kW e inductancia variable.

En el diseño del generador, se ubicaron siete pares de bobinas planas a ambos lados del marco, en cuya cavidad giraba un disco ferromagnético con protuberancias. Cuando un motor impulsa el disco para que gire, sus protuberancias se mueven periódicamente dentro y fuera del espacio entre cada par de bobinas, cambiando así la inductancia y excitando las oscilaciones.