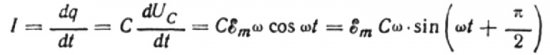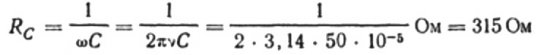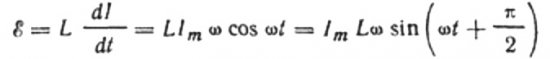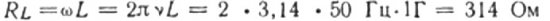Resistencia capacitiva e inductiva en un circuito de corriente alterna

Si incluimos un capacitor en un circuito de CC, encontramos que tiene una resistencia infinita porque una corriente continua simplemente no puede pasar a través del dieléctrico entre las placas, ya que un dieléctrico, por definición, no conduce una corriente eléctrica directa.

Un condensador rompe el circuito de CC. Pero si ahora se incluye el mismo capacitor en el circuito de corriente alterna, resulta que su capacitor no parece romperse por completo, simplemente alterna y se carga, es decir, la carga eléctrica se mueve y la corriente en el circuito externo es mantenido

Basándonos en la teoría de Maxwell, en este caso podemos decir que la corriente de conducción alterna dentro del capacitor todavía está cerrada, solo que en este caso, por la corriente de polarización. Esto significa que el capacitor en el circuito de CA actúa como un tipo de resistencia de valor finito. Esta resistencia se llama capacitivo.

La práctica ha demostrado durante mucho tiempo que la cantidad de corriente alterna que fluye a través de un conductor depende de la forma de ese conductor y de las propiedades magnéticas del medio que lo rodea.Con un cable recto, la corriente será máxima, y ​​si el mismo cable se enrolla en una bobina con un gran número de vueltas, la corriente será menor.

Y si se introduce un núcleo ferromagnético en la misma bobina, la corriente disminuirá aún más. Por lo tanto, el cable proporciona corriente alterna no solo con una resistencia óhmica (activa), sino también con una resistencia adicional, dependiendo de la inductancia del cable.Esta resistencia se llama inductivo.

Su significado físico es que una corriente cambiante en un conductor de cierta inductancia inicia una FEM de autoinducción en ese conductor, que tiende a evitar cambios en la corriente, es decir, tiende a reducir la corriente. Esto es equivalente a aumentar la resistencia del cable.

Capacitancia en el circuito de CA

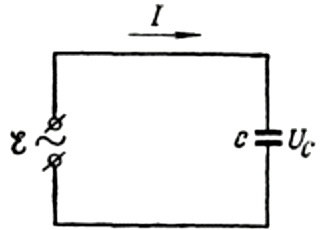
Primero, hablemos de la resistencia capacitiva con más detalle. Supongamos que un capacitor de capacitancia C está conectado a una fuente de corriente alterna sinusoidal, entonces la FEM de esta fuente se describirá mediante la siguiente fórmula:

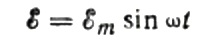
Ignoraremos la caída de voltaje a través de los cables de conexión, ya que generalmente es muy pequeña y se puede considerar por separado si es necesario. Supongamos ahora que el voltaje a través de las placas del condensador es igual al voltaje de la fuente de CA. Entonces:

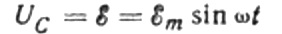
En un momento dado, la carga de un capacitor depende de su capacitancia y del voltaje entre sus placas. Luego, dada la fuente conocida que se mencionó anteriormente, obtenemos una expresión para encontrar la carga en las placas del capacitor por el voltaje de la fuente:

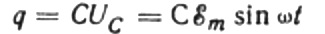
Supongamos que durante un tiempo infinitesimal dt la carga del condensador cambia en dq, entonces fluirá una corriente I a través de los cables desde la fuente hasta el condensador igual a:

El valor de la amplitud de corriente será igual a:

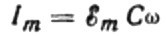
Entonces la expresión final para la corriente será:

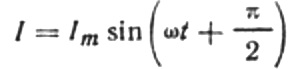
Reescribamos la fórmula de amplitud actual de la siguiente manera:

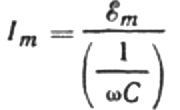
Esta relación es la ley de Ohm, donde el recíproco del producto de la frecuencia angular y la capacitancia desempeña el papel de resistencia, y en realidad es una expresión para encontrar la capacitancia de un capacitor en un circuito de corriente alterna sinusoidal:

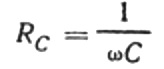
Esto significa que la resistencia capacitiva es inversamente proporcional a la frecuencia angular de la corriente y la capacitancia del capacitor. Es fácil comprender el significado físico de esta dependencia.

Cuanto mayor sea la capacitancia del capacitor en el circuito de CA y más a menudo cambie la dirección de la corriente en ese circuito, finalmente pasará más carga total por unidad de tiempo a través de la sección transversal de los cables que conectan el capacitor a la fuente de CA. Esto significa que la corriente es proporcional al producto de la capacitancia y la frecuencia angular.

Por ejemplo, calculemos la capacitancia de un capacitor con una capacidad eléctrica de 10 microfaradios para un circuito de corriente alterna sinusoidal con una frecuencia de 50 Hz:

Si la frecuencia fuera de 5000 Hz, entonces el mismo condensador presentaría una resistencia de unos 3 ohmios.

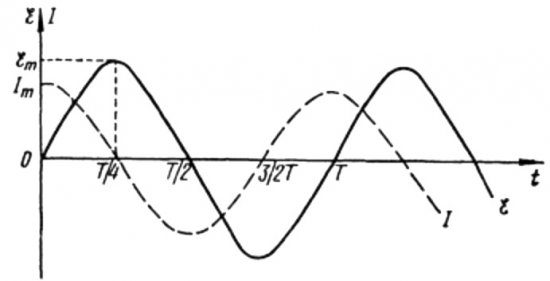
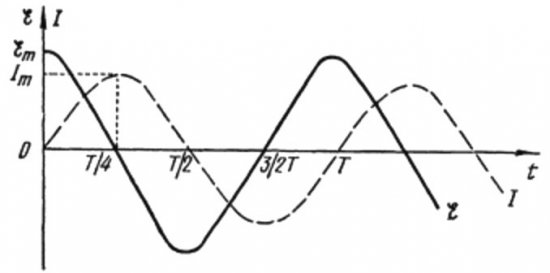
De las fórmulas anteriores queda claro que la corriente y el voltaje en un circuito de CA con un capacitor siempre cambian en diferentes fases. La fase de corriente adelanta a la fase de tensión en pi/2 (90 grados). Esto significa que la corriente máxima en el tiempo siempre existe un cuarto de período antes que el voltaje máximo. Por lo tanto, a través de la resistencia capacitiva, la corriente se adelanta al voltaje en una cuarta parte del período de tiempo, o en 90 grados en fase.

Expliquemos el significado físico de este fenómeno.En el primer instante de tiempo, el capacitor está completamente descargado, por lo que el más mínimo voltaje que se le aplica ya mueve las cargas en las placas del capacitor, creando una corriente.

A medida que el capacitor se carga, el voltaje en sus placas aumenta, lo que evita que la carga fluya más, por lo que la corriente en el circuito disminuye a pesar de los aumentos adicionales en el voltaje aplicado a las placas.

Esto significa que si en el momento inicial la corriente era máxima, cuando el voltaje alcance su máximo después de un cuarto de período, la corriente se detendrá por completo.

Al comienzo del período, la corriente es máxima y el voltaje es mínimo y comienza a aumentar, pero después de una cuarta parte del período, el voltaje alcanza un máximo, pero la corriente ya ha caído a cero en este momento. Por lo tanto, resulta que el voltaje se adelanta al voltaje en una cuarta parte del período.

Resistencia inductiva de CA

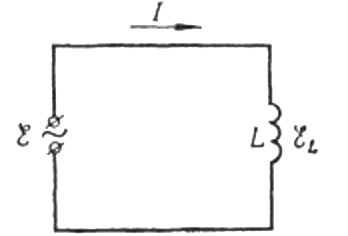
Ahora volvamos a la resistencia inductiva. Suponga que una corriente sinusoidal alterna fluye a través de una bobina de inductancia. Se puede expresar como:

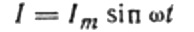
La corriente se debe al voltaje alterno aplicado a la bobina. Esto significa que en la bobina aparecerá una FEM de autoinducción, que se expresa de la siguiente manera:

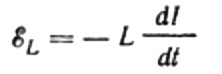
Nuevamente, ignoramos la caída de voltaje a través de los cables que conectan la fuente EMF a la bobina. Su resistencia óhmica es muy baja.

Deje que el voltaje alterno aplicado a la bobina en cualquier instante de tiempo esté completamente equilibrado por la EMF resultante de la autoinducción igual a ella en magnitud pero de dirección opuesta:

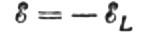
Entonces tenemos derecho a escribir:

Dado que la amplitud del voltaje aplicado a la bobina es:

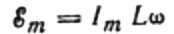
obtenemos:

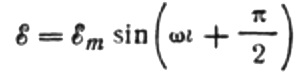
Expresemos la corriente máxima de la siguiente manera:

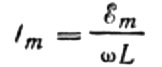
Esta expresión es esencialmente la ley de Ohm. Una cantidad igual al producto de la inductancia y la frecuencia angular juega aquí el papel de resistencia y no es más que la resistencia inductiva del inductor:

Entonces, la resistencia inductiva es proporcional a la inductancia de la bobina y la frecuencia angular de la corriente alterna a través de esa bobina.

Esto se debe al hecho de que la resistencia inductiva se debe a la influencia de la FEM de autoinducción en el voltaje de la fuente, la FEM de autoinducción tiende a reducir la corriente y, por lo tanto, genera resistencia en el circuito. La magnitud de la fem de autoinducción, como se sabe, es proporcional a la inductancia de la bobina y la tasa de cambio de la corriente a través de ella.

Por ejemplo, calculemos la resistencia inductiva de una bobina con una inductancia de 1 H, que está incluida en un circuito con una frecuencia de corriente de 50 Hz:

Si la frecuencia de la bola fuera de 5000 Hz, entonces la resistencia de la misma bobina sería de aproximadamente 31 400 ohmios.Recuerde que la resistencia óhmica del cable de la bobina suele ser de unos pocos ohmios.

De las fórmulas anteriores, es obvio que los cambios en la corriente a través de la bobina y el voltaje en ella ocurren en diferentes fases, y la fase de la corriente siempre es menor que la fase del voltaje en pi / 2. Por lo tanto, el la corriente máxima ocurre un cuarto de período después del inicio de la tensión máxima.

En la resistencia inductiva, la corriente tiene un retraso de 90 grados con respecto al voltaje debido al efecto de frenado de la EMF autoinducida, que evita que la corriente cambie (tanto aumente como disminuya), por lo que la corriente máxima se observa en el circuito con la bobina más tarde. que el voltaje máximo.

Acción combinada de bobina y capacitor

Si conecta una bobina con un capacitor en serie con un circuito de corriente alterna, entonces el voltaje de la bobina adelantará el voltaje del capacitor en el tiempo medio período, es decir, 180 grados en fase.

Las resistencias capacitiva e inductiva se llaman reactivos… La energía no se gasta en la resistencia reactiva como en la resistencia activa. La energía almacenada en el capacitor regresa periódicamente a la fuente cuando desaparece el campo eléctrico en el capacitor.

Lo mismo ocurre con una bobina: como el campo magnético de la bobina es creado por la corriente, la energía en ella se acumula durante un cuarto del período, y durante el siguiente cuarto del período regresa a la fuente. En este artículo hemos hablado de la corriente alterna sinusoidal, para la que se siguen estrictamente estas normas.

En los circuitos sinusoidales de CA, los inductores con núcleo se denominan sofocantese utilizan tradicionalmente para limitar la corriente. Su ventaja sobre los reóstatos es que la energía no se disipa en grandes cantidades en forma de calor.