¿Qué es un suministro eléctrico?

El hombre moderno se encuentra constantemente con la electricidad en la vida cotidiana y en el trabajo, utiliza dispositivos que consumen corriente eléctrica y dispositivos que la generan. Al trabajar con ellos, siempre debe tener en cuenta sus capacidades inherentes a las características técnicas.

Uno de los principales indicadores de cualquier dispositivo eléctrico es una cantidad física como energía eléctrica... Se acostumbra llamar a la intensidad o velocidad de generación, transmisión o conversión de electricidad en otros tipos de energía, por ejemplo, calor, luz, mecánico.

El transporte o transferencia de energía eléctrica de gran volumen para fines industriales se realiza de acuerdo con líneas eléctricas de alta tensión.

Transformación energía eléctrica se lleva a cabo en las subestaciones transformadoras.

El consumo de electricidad se produce en dispositivos domésticos e industriales para diversos fines. Uno de sus tipos comunes son lámparas incandescentes de varias clasificaciones.

La potencia eléctrica de los generadores, las líneas eléctricas y los consumidores en los circuitos de CC y CA tiene el mismo significado físico, que se expresa simultáneamente en diferentes proporciones según la forma de las señales compuestas. Para definir los patrones generales, nociones de valores instantáneos... Vuelven a enfatizar la dependencia de la tasa de transformación de la electricidad con el tiempo.

Determinación de la potencia eléctrica instantánea

En ingeniería eléctrica teórica, para derivar las relaciones básicas entre corriente, voltaje y potencia, se utilizan sus imágenes en forma de valores instantáneos, que se fijan en un momento determinado.

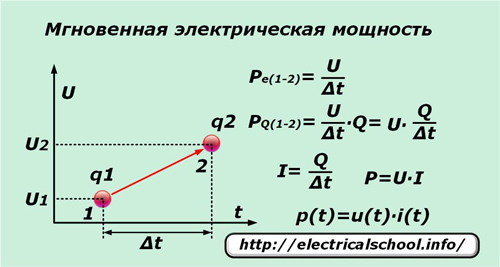
Si en un período de tiempo muy corto ∆t una sola carga elemental q bajo la influencia del voltaje U se mueve del punto «1» al punto «2», entonces realiza un trabajo igual a la diferencia de potencial entre estos puntos. Dividiéndolo por el intervalo de tiempo ∆t, obtenemos la expresión de la potencia instantánea por unidad de carga Pe (1-2).

Dado que no solo la carga individual se mueve bajo la acción del voltaje aplicado, sino también todas las adyacentes que están bajo la influencia de esta fuerza, cuyo número está convenientemente representado por el número Q, entonces el valor instantáneo de la potencia PQ (1-2) se puede escribir para ellos.

Después de realizar transformaciones simples, obtenemos la expresión de la potencia P y la dependencia de su valor instantáneo p (t) de los componentes del producto de la corriente instantánea i (t) y el voltaje u (t).

Determinación de la potencia eléctrica constante

V circuitos de CC la magnitud de la caída de voltaje en la sección del circuito y la corriente que fluye a través de él no cambia y permanece estable, igual a los valores instantáneos.Por lo tanto, la potencia en este circuito se puede determinar multiplicando estos valores o dividiendo el trabajo perfecto A por el período de su ejecución, como se muestra en la imagen explicativa.

Determinación de la potencia eléctrica en corriente alterna

Las leyes de variación sinusoidal de corrientes y voltajes transmitidos a través de redes eléctricas imponen su influencia en la expresión de potencia en tales circuitos. Aquí entra en juego la potencia aparente, que se describe mediante el triángulo de potencia y consta de componentes activos y reactivos.

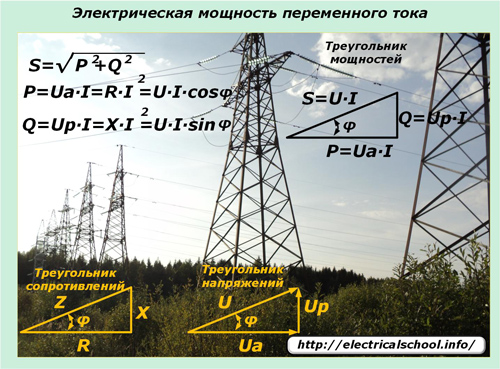
Una corriente eléctrica sinusoidal cuando pasa a través de líneas eléctricas con tipos mixtos de cargas en todas las secciones no cambia la forma de su armónico y la caída de voltaje en las cargas reactivas cambia de fase en una dirección determinada. Las expresiones de valor de momento ayudan a comprender el efecto de las cargas aplicadas en el cambio de potencia en el circuito y su dirección.

Al mismo tiempo, preste atención de inmediato al hecho de que la dirección del flujo de corriente del generador al consumidor y la potencia transmitida a través del circuito creado son cosas completamente diferentes, que en algunos casos pueden no solo no coincidir, sino también ser dirigida en direcciones opuestas.

Considere estas relaciones en su manifestación pura e ideal para diferentes tipos de cargas:

• activo;

• capacitivo;

• inductivo.

Disipación de potencia de carga activa

Supondremos que el generador produce un voltaje sinusoidal ideal u que se aplica a la resistencia puramente activa del circuito. El amperímetro A y el voltímetro V miden la corriente I y el voltaje U cada vez que t.

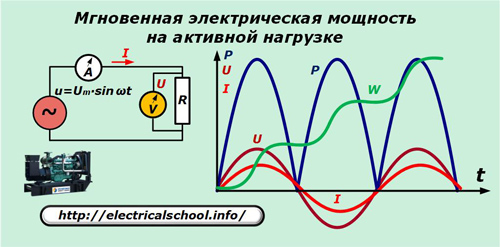
El gráfico muestra que las sinusoides de la corriente y la caída de voltaje a través de la resistencia activa coinciden en frecuencia y fase, haciendo las mismas oscilaciones. La fuerza expresada por su producto oscila al doble de la frecuencia y siempre es positiva.

p = u ∙ i = Um ∙ senωt ∙ Um / R ∙ senωt = Um2/ R ∙ sen2ωt = Um2/ 2R ∙ (1-cos2ωt).

Si vamos a la expresión tensión de funcionamiento, entonces obtenemos: p = P ∙ (1-cos2ωt).

Luego integraremos la potencia durante el período de una oscilación T y podremos notar que la ganancia de energía ∆W durante este intervalo aumenta. Con el tiempo, la resistencia continúa consumiendo nuevas porciones de electricidad, como se muestra en el gráfico.

Con cargas reactivas, las características del consumo de energía son diferentes, tienen una forma diferente.

Disipación de potencia capacitiva

En el circuito eléctrico del generador, reemplace el elemento resistivo con un capacitor de capacitancia C.

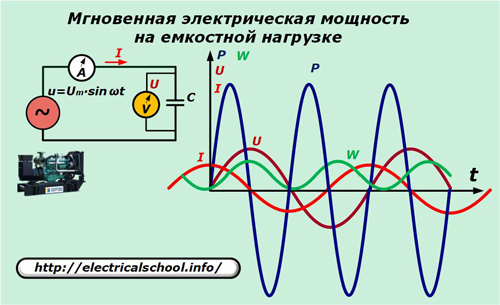
La relación entre la corriente y la caída de voltaje en la capacitancia se expresa por la relación: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Multiplicamos los valores de las expresiones instantáneas de corriente con voltaje y obtenemos el valor de la potencia que consume la carga capacitiva.

p = u ∙ i = Um ∙ senωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ senωt ∙ cosωt = Um2/ (2X° C) ∙ sen2ωt = U2/ (2X° C) ∙ sen2ωt.

Aquí puede ver que la potencia fluctúa alrededor de cero al doble de la frecuencia del voltaje aplicado. Su valor total para el período armónico, así como la ganancia de energía, es cero.

Esto significa que la energía se mueve a lo largo del circuito cerrado del circuito en ambas direcciones, pero no realiza trabajo.Tal hecho se explica por el hecho de que cuando el voltaje de la fuente aumenta en valor absoluto, la potencia es positiva y el flujo de energía a través del circuito se dirige al contenedor, donde se acumula la energía.

Después de que el voltaje pasa a la sección armónica descendente, la energía regresa del capacitor al circuito a la fuente. No se realiza ningún trabajo útil en ninguno de los dos procesos.

Disipación de potencia en una carga inductiva

Ahora, en el circuito de suministro, reemplace el capacitor con inductancia L.

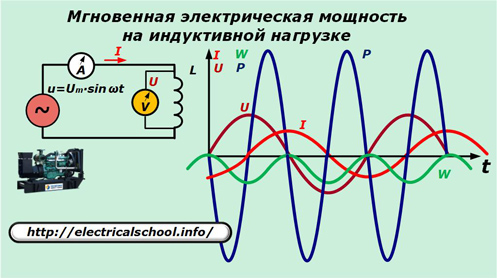
Aquí, la corriente a través de la inductancia se expresa mediante la relación:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Entonces obtenemos

p = u ∙ i = Um ∙ senωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ senωt ∙ cosωt = -Um2/ (2ХL) ∙ sen2ωt = -U2/ (2ХL) ∙ sen2ωt.

Las expresiones resultantes nos permiten ver la naturaleza del cambio de dirección de la potencia y el aumento de energía sobre la inductancia, que realiza las mismas oscilaciones inútiles para realizar trabajo, que sobre la capacitancia.

La potencia liberada en las cargas reactivas se denomina componente reactivo. En condiciones ideales, cuando los cables de conexión no tienen resistencia activa, parece inofensivo y no causa ningún daño. Pero en condiciones de potencia real, los transitorios periódicos y las fluctuaciones de potencia reactiva provocan el calentamiento de todos los elementos activos, incluidos los cables de conexión, por lo que se consume algo de energía y el valor de la potencia total aplicada de la fuente disminuye.

La principal diferencia entre el componente reactivo de la potencia es que no realiza ningún trabajo útil, pero provoca pérdidas de energía eléctrica y cargas excesivas en los equipos, que son especialmente peligrosos en situaciones críticas.

Por estas razones, para eliminar la influencia de la potencia reactiva, especialmente sistemas técnicos para su compensación.

Distribución de potencia con carga mixta

Como ejemplo, usamos la carga de un generador con una característica capacitiva activa.

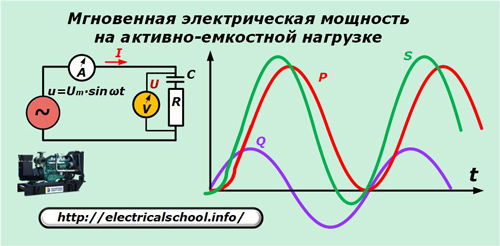
Para simplificar la imagen, las sinusoides de corrientes y voltajes no se muestran en el gráfico dado, pero debe tenerse en cuenta que con una naturaleza activa-capacitiva de la carga, el vector de corriente conduce al voltaje.

p = u ∙ i = Um ∙ senωt ∙ ωC ∙ Im ∙ sen (ωt + φ).

Después de las transformaciones obtenemos: p = P ∙ (1- cos 2ωt) + Q ∙ sen2ωt.

Estos dos términos en la última expresión son los componentes activo y reactivo de la potencia aparente instantánea. Sólo el primero de ellos hace un trabajo útil.

Herramientas de medición de potencia

Para analizar el consumo de electricidad y calcularlo, se utilizan dispositivos de medición, que durante mucho tiempo se han llamado «Contadores»… Su trabajo se basa en medir los valores efectivos de corriente y voltaje y multiplicarlos automáticamente con una salida de información.

Los medidores muestran el consumo de energía contando el tiempo de funcionamiento de los aparatos eléctricos de forma incremental desde el momento en que el medidor se enciende bajo carga.

Para medir el componente activo de la potencia en los circuitos de CA, vatímetros, y reactivo - varmetros. Tienen diferentes denominaciones de unidades:

• vatio (W, W);

• var (var, var, var).

Para determinar el consumo total de energía, es necesario calcular su valor utilizando la fórmula del triángulo de potencia en base a las lecturas del vatímetro y el varímetro. Se expresa en sus propias unidades: voltios-amperios.

Las designaciones aceptadas de las unidades de cada uno ayudan a los electricistas a juzgar no solo su valor, sino también la naturaleza del componente de potencia.