Ley de Ohm para un circuito magnético.

Si no hubiera flujos magnéticos, es poco probable que existiera la ingeniería eléctrica moderna. El funcionamiento de generadores y motores eléctricos, electroimanes y transformadores, instrumentos de medida y sensores Hall se basa en el aprovechamiento del campo magnético y las propiedades del flujo magnético.

Para concentrar y potenciar el flujo magnético recurren al uso de materiales ferromagnéticos. Los materiales ferromagnéticos se producen núcleos magnéticos — cuerpos de las formas y tamaños requeridos, núcleos para dirigir flujos magnéticos de uno u otro tamaño en la dirección requerida. Dichos cuerpos, dentro de los cuales pasan líneas cerradas de inducción magnética, se denominan circuitos magnéticos.

Las propiedades conocidas del campo magnético permiten calcular los flujos magnéticos en varios circuitos magnéticos. Pero para el trabajo práctico, es mucho más conveniente recurrir a consecuencias generales y leyes de circuitos magnéticos derivadas de las leyes del campo magnético, en lugar de usar estas leyes directamente cada vez. Aplicar ciertas reglas a los circuitos magnéticos es más conveniente para resolver problemas prácticos típicos.

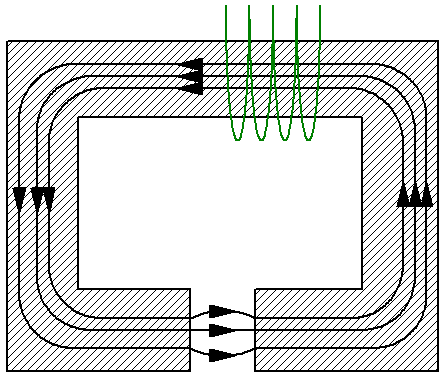
Por ejemplo, considere un circuito magnético simple que consta de un yugo no ramificado de sección transversal S, que a su vez está hecho de un material con permeabilidad mu… El yugo tiene un espacio no magnético de la misma área S, por ejemplo aire, y la permeabilidad magnética en el espacio — mu1 — es diferente de la permeabilidad magnética del yugo. Aquí puede ver la línea media de inducción y aplicarle el teorema de la tensión magnética:

Dado que las líneas de inducción magnética son continuas en todo el circuito, la magnitud del flujo magnético tanto en el yugo como en el espacio es la misma. Ahora usamos las fórmulas para inducción magnética B y para el flujo magnético F para expresar la fuerza H del campo magnético en términos del flujo magnético F.

El siguiente paso es sustituir las expresiones resultantes en la fórmula anterior del teorema del flujo magnético:

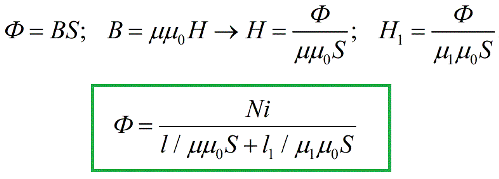
Obtuvimos una fórmula muy similar a la conocida en ingeniería eléctrica Ley de Ohm para una sección de un circuito cerrado, y el papel de la EMF aquí lo desempeña la cantidad iN, llamada fuerza magnetomotriz (o MDF) por analogía con la fuerza electromotriz. En el sistema SI, la fuerza magnetomotriz se mide en amperios.

La suma en el denominador no es más que una analogía de la resistencia eléctrica total de un circuito eléctrico y, en consecuencia, para un circuito magnético se denomina resistencia magnética total. Los términos en el denominador son las resistencias magnéticas de secciones individuales del circuito magnético.

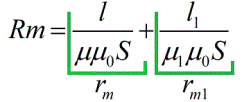
Las resistencias magnéticas dependen de la longitud del circuito magnético, su área de sección transversal y la permeabilidad magnética (similar a la conductividad eléctrica para la ley de Ohm habitual).Como resultado, puedes escribir la fórmula de la ley de Ohm, solo para un circuito magnético:

Es decir, la formulación de la ley de Ohm en relación a un circuito magnético suena así: «en un circuito magnético sin ramificación, el flujo magnético es igual al cociente de la división de MDS por la resistencia magnética total del circuito».

Es obvio a partir de las fórmulas que la resistencia magnética en NE se mide en amperios weber, y la resistencia magnética total de un circuito magnético es numéricamente igual a la suma de las resistencias magnéticas de las partes de ese circuito magnético.

La situación descrita es válida para un circuito magnético no ramificado que incluye cualquier número de partes, siempre que el flujo magnético penetre sucesivamente en todas estas partes. Si los núcleos magnéticos están conectados en serie, entonces la resistencia magnética total se encuentra sumando las resistencias magnéticas de las partes.

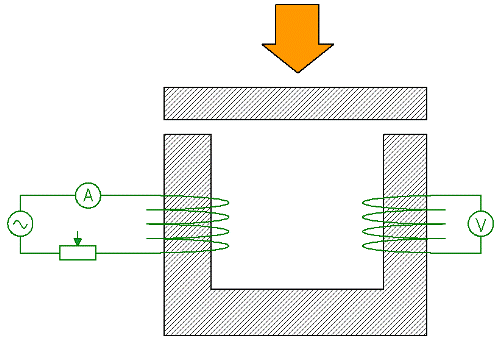
Considere ahora un experimento que demuestra el efecto de la reluctancia de partes de un circuito sobre la reluctancia total de un circuito.Un circuito magnético en forma de U es magnetizado por la bobina 1, que se alimenta (corriente alterna) a través de un amperímetro y un reóstato. Se induce un EMF en el devanado secundario 2, y las lecturas del voltímetro conectado al devanado, como saben, son proporcionales al flujo magnético en el circuito magnético.

Si ahora mantiene la corriente en el devanado primario sin cambios regulándola con un reóstato, y al mismo tiempo presiona la placa de hierro contra el circuito magnético de arriba, después de que la resistencia magnética total del circuito se reduzca considerablemente, la lectura de la voltímetro aumentará en consecuencia.

Por supuesto, los términos anteriores, como "magnetorresistencia" y "fuerza magnetomotriz", son conceptos formales, ya que nada en el flujo magnético se mueve, no hay partículas en movimiento, es solo una representación visual (como un modelo de flujo de fluido) de una comprensión más clara de las leyes...

El significado físico del experimento anterior y otros experimentos similares es comprender cómo la introducción de espacios no magnéticos y materiales magnéticos en el circuito magnético afecta el flujo magnético en el circuito magnético.

Introduciendo, por ejemplo, un imán en un circuito magnético, añadimos corrientes moleculares adicionales a los cuerpos ya contenidos en el circuito, que introducen flujos magnéticos adicionales. Conceptos formales como «resistencia magnética» y «fuerza magnetomotriz» resultan muy convenientes a la hora de resolver un problema práctico, por lo que se utilizan con éxito en ingeniería eléctrica.