El principio y los métodos de determinación indirecta del factor de potencia en el circuito de corriente alterna.
Factor de potencia o coseno phi, respecto al usuario de corriente alterna sinusoidal, es la relación entre el consumo de potencia activa P y la potencia total S que se suministra a este usuario desde la red.
Potencia total S, en el caso general, se puede definir como el producto de los valores efectivos (raíz cuadrática media) de la corriente I y el voltaje U en el circuito considerado, y la potencia activa P, como irreversiblemente consumida por el usuario para el funcionamiento de obra.
Potencia reactiva Q, aunque forma parte de la potencia total, sin embargo, no se consume para realizar el trabajo, sino que solo participa en la creación de campos eléctricos y magnéticos alternos en algunos elementos del circuito del usuario.
excepto medición directa del factor de potencia uso de dispositivos electrodinámicos — medidores de fase, existen métodos indirectos bastante lógicos que le permiten comprender matemáticamente con precisión el valor de esta cantidad eléctrica tan importante que caracteriza al usuario en un circuito de corriente alterna sinusoidal.
Veamos los datos métodos indirectos en detalles, Entendamos el principio de la medición indirecta del factor de potencia.
Método de voltímetro, amperímetro y vatímetro
vatímetro electrodinámico con resistencia activa adicional en el circuito de su bobina móvil indica el valor de potencia extremadamente activa consumida en el circuito de CA P.
Si ahora, usando un voltímetro y un amperímetro, medimos los valores promedio de la corriente I y el voltaje U que actúan en el circuito de la carga en estudio, al multiplicar estos dos parámetros, obtendremos solo la potencia total S .
Entonces, el factor de potencia (coseno phi) de una carga dada se puede encontrar fácilmente usando la fórmula:
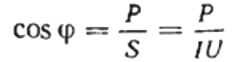
Aquí, si lo desea, también puede encontrar el valor de la potencia reactiva Q, la resistencia total del circuito z Ley de Ohm, así como resistencia activa y reactiva, simplemente construyendo o representando un triángulo de resistencia, y luego usando el teorema de Pitágoras:
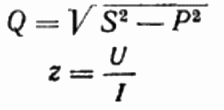
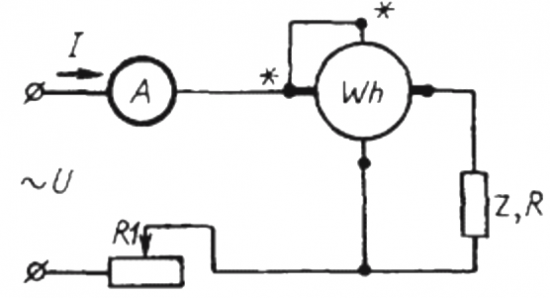
Método de contador y amperímetro
Para usar este método, es necesario ensamblar un circuito en el que el más simple esté conectado en serie con la carga Z y el amperímetro. medidor de electricidad ¿Qué?
Durante un cierto tiempo t, del orden de un minuto, será necesario calcular el número de revoluciones del disco N, que mostrará la cantidad de energía activa gastada durante un tiempo dado (es decir, teniendo en cuenta la Factor de potencia).
Aquí: el número de revoluciones del disco N, el coeficiente k es la cantidad de energía por revolución, I y U son la corriente y el voltaje rms respectivamente, t es el tiempo para contar las revoluciones, el coseno phi es el factor de potencia:
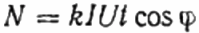
Entonces, en lugar del usuario Z estudiado, se incluye en el circuito la carga activa R a través del mismo contador, pero no directamente, sino a través del reóstato R1 (consiguiendo la misma corriente I que en el primer caso, con el usuario Z). El número de revoluciones del disco N1 se mantiene durante el mismo tiempo t. Pero aquí, dado que la carga está activa, el coseno phi (factor de potencia) es ciertamente igual a 1. Por lo tanto:
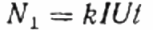
Luego se registra la relación de revoluciones del contador de disco para el mismo período de tiempo en el primer y segundo caso, este será el coseno phi, es decir, el factor de potencia de la primera carga (respecto a una carga puramente activa con el mismo actual):
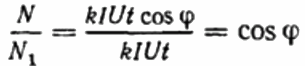
Método de tres amperímetros
Para determinar el factor de potencia en un circuito de corriente sinusoidal utilizando tres amperímetros, primero debe ensamblar el siguiente circuito:
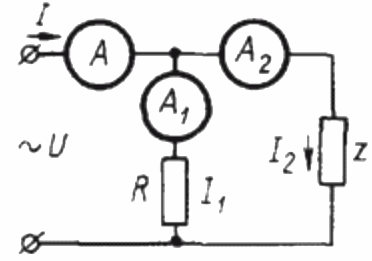
Aquí Z es una carga cuyo factor de potencia debe determinarse y R es una carga puramente activa.
Dado que la carga R es puramente activa, la corriente I1 en cualquier instante de tiempo está en fase con la tensión alterna aplicada a esta carga U. En este caso, la corriente I es igual a la suma geométrica de las corrientes I1 e I2. Ahora construiremos en base a esta posición un diagrama vectorial de las corrientes:
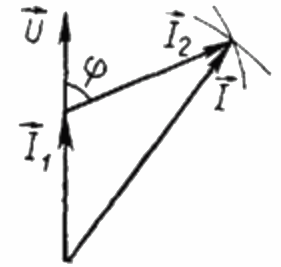
En el diagrama vectorial de las corrientes, el ángulo agudo entre la corriente I1 y la corriente I2 es el ángulo phi, cuyo coseno (de hecho, el valor del factor de potencia) se puede encontrar en una tabla especial de valores de funciones trigonométricas o calculadas por la fórmula:
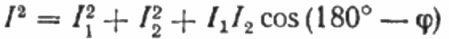
A partir de aquí podemos expresar el coseno phi, es decir, el factor de potencia deseado:
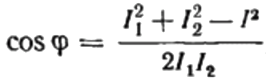
El signo del factor de potencia encontrado ("+" o "-") indicará la naturaleza de la carga. Si el factor de potencia (coseno phi) es negativo, la carga es de naturaleza capacitiva. Si el factor de potencia es un valor positivo, entonces la naturaleza de la carga es inductiva.