Teoría de autómatas, autómatas finitos
La estructura, el diseño y el principio de funcionamiento de varias máquinas están determinados en gran medida por su propósito funcional. Distinguir entre máquinas tecnológicas, de transporte, informáticas, militares y otras. Los complejos automáticos completos diseñados para realizar procesos tecnológicos complejos se introducen ampliamente en diversas industrias. Los autómatas están diseñados y construidos para realizar varias funciones lógicas (máquinas lógicas).
Teoría de los autómatas — sección de cibernética, que surgió bajo la influencia de los requisitos de la tecnología de las computadoras digitales y las máquinas de control. Los autómatas discretos estudiados en la teoría de autómatas son modelos abstractos de sistemas reales (tanto técnicos como biológicos) que procesan información discreta (digital) en pasos de tiempo discretos.
La teoría de los autómatas se basa en conceptos matemáticos precisos que formalizan ideas intuitivas sobre el funcionamiento (comportamiento) del autómata y sobre su estructura (estructura interna).
En este caso, la transformación de la información siempre se entiende como una operación que transforma secuencias de entrada compuestas por letras del alfabeto de entrada en secuencias de salida compuestas por letras del alfabeto de salida.
El aparato de lógica matemática, álgebra, teoría de probabilidades, combinatoria y teoría de grafos es ampliamente utilizado.
El problema con la teoría de autómatas en algunas de sus partes (teoría estructural de autómatas) creció de la teoría de los circuitos de contacto de relé, que comenzó a tomar forma a finales de la década de 1930. inclusivo metodos de algebra logica.

En la teoría estructural de los autómatas se estudian diferentes tipos de esquemas, diseñados para describir cómo se crea un autómata complejo a partir de componentes más simples (elementos) correctamente conectados en un sistema.
Otra dirección, llamada teoría abstracta de los autómatas, estudia el comportamiento de los autómatas (es decir, la naturaleza de la transformación de la información que llevan a cabo), mientras se abstrae de los detalles de su estructura interna, y surgió en la década de 1950.
En el marco de la teoría abstracta de los autómatas, el contenido de los conceptos "autómata" y "máquina" se agota esencialmente en la descripción estándar de la transformación de la información que lleva a cabo un autómata. Tal transformación puede ser determinista, pero también puede ser de naturaleza probabilística.
Las más estudiadas son las máquinas deterministas (autómatas), que incluyen autómatas finitos, el principal objeto de estudio en la teoría de los autómatas.
Una máquina de estados finitos se caracteriza por una cantidad limitada de memoria (el número de estados internos) y se define mediante una función de transición.Con una idealización razonable, todas las máquinas matemáticas modernas e incluso el cerebro, desde el punto de vista de su funcionamiento, pueden considerarse autómatas finitos.
Los términos "máquina secuencial", "autómata de Milly", "autómata de Moore" se utilizan en la literatura (y no de manera uniforme por todos los autores) como sinónimos del término "autómata finito" o para enfatizar ciertas características en las funciones de transición de un finito. autómata.
Automata con memoria ilimitada es una máquina de Turing capaz de realizar (potencialmente) cualquier transformación de información eficiente. El concepto de "máquina de Turing" surgió antes que el concepto de "máquina de estados finitos" y se estudia principalmente en la teoría de algoritmos.
La teoría de los autómatas abstractos está estrechamente relacionada con teorías algebraicas bien conocidas, por ejemplo, la teoría de semigrupos. Desde un punto de vista aplicado, son de interés los resultados que caracterizan la transformación de información en un autómata en términos de tamaño de memoria.
Es el caso, por ejemplo, de problemas con experimentos sobre autómatas (obras de E.F. Moore, etc.), donde a partir de los resultados de las experimentos
Otra tarea es calcular los periodos de las secuencias de salida, en base a la información disponible sobre el tamaño de la memoria del autómata y los periodos de las secuencias de entrada.
De gran importancia es el desarrollo de métodos para minimizar la memoria de máquinas de estados finitos y estudiar su comportamiento en entornos aleatorios.
En la teoría de autómatas abstractos, el problema de síntesis es el siguiente.En términos de algún lenguaje claramente formalizado, las condiciones están escritas para el comportamiento del autómata diseñado (para el evento representado en el autómata). En este caso, es necesario desarrollar métodos que de acuerdo a cada condición escrita:
1) averiguar si existe una máquina de estados tal que la información transformada por ella cumpla esta condición;
2) en caso afirmativo, entonces se construyen las funciones de transición de dicha máquina de estados finitos o se estima su tamaño de memoria.
La solución de la tarea de síntesis en tal formulación presupone la creación preliminar de un lenguaje conveniente para registrar las condiciones operativas de un autómata con algoritmos convenientes para la transición de registro a funciones transitivas.
En la teoría estructural de autómatas, el problema de síntesis consiste en construir una cadena de elementos de un tipo dado que realice un autómata finito dado por sus funciones de transición. En este caso, suelen enunciar algún criterio de optimalidad (por ejemplo, el número mínimo de elementos) y buscan obtener un esquema óptimo.
Como resultó más tarde, esto significa que algunos de los métodos y conceptos desarrollados anteriormente en relación con los circuitos de contacto de relé son aplicables a circuitos de otro tipo.
En relación con el desarrollo de las tecnologías electrónicas, los más difundidos son los esquemas de elementos funcionales (redes lógicas). Un caso especial de redes lógicas son las redes neuronales abstractas, cuyos elementos se denominan neuronas.
Se han desarrollado muchos métodos de síntesis, según el tipo de circuitos y la transformación de información a la que están destinados (Síntesis de dispositivos de relé).
Mirar -Minimización de circuitos combinacionales, mapas de Carnot, síntesis de circuitos
Máquina de estados finitos — un modelo matemático de un sistema de control con un tamaño de memoria fijo (que no puede aumentar durante la operación).
El concepto de máquina de estados finitos es una abstracción matemática que caracteriza las características generales de un conjunto de sistemas de control (por ejemplo, un dispositivo de relé de bucle múltiple). Todos estos sistemas tienen características comunes que son naturales para aceptar como la definición de un autómata finito.
Cada autómata completo tiene una entrada expuesta a influencias externas y elementos internos. Tanto para los elementos de entrada como para los internos, hay un número fijo de estados discretos que pueden tomar.
El cambio en los estados de los elementos de entrada e internos ocurre en momentos discretos en el tiempo, los intervalos entre los cuales se denominan tics. El estado interno (el estado de las partes internas) al final de la cinta está determinado completamente por el estado interno y el estado de la entrada al comienzo de la cinta.
Todas las demás definiciones de un autómata finito se pueden reducir a esta característica, en particular las definiciones que suponen que un autómata finito tiene una salida que depende del estado interno del autómata en un momento dado.
En términos de tal característica, la naturaleza de sus entradas y estados internos es irrelevante para la descripción de un autómata completo. En lugar de entradas y estados, solo puede mirar sus números en una numeración aleatoria.
La máquina de estado se establecerá si se especifica la dependencia de su número de estado interno en el número de estado interno anterior y el número de estado de entrada anterior. Tal tarea puede ser en forma de una mesa final.
Otra forma común de definir un autómata completo es la construcción de los llamados diagramas de transición. Los estados de entrada a menudo se denominan simplemente entradas, y los estados internos son simplemente estados.
Una máquina de estados finitos puede ser un modelo tanto de dispositivos técnicos como de algunos sistemas biológicos. Los autómatas del primer tipo son, por ejemplo, dispositivos de relé y varias computadoras electrónicas, incl. controladores lógicos programables.
En el caso de un dispositivo de relé, el papel de los estados de entrada lo desempeñan las combinaciones de estados de los elementos sensibles del dispositivo de relé (cada combinación de tales estados es un «estado complejo», caracterizado por una indicación de todos los elementos sensibles de estos estados discretos que tienen en un momento dado). De manera similar, las combinaciones de estados de los elementos intermedios de un dispositivo de relé actúan como estados internos.
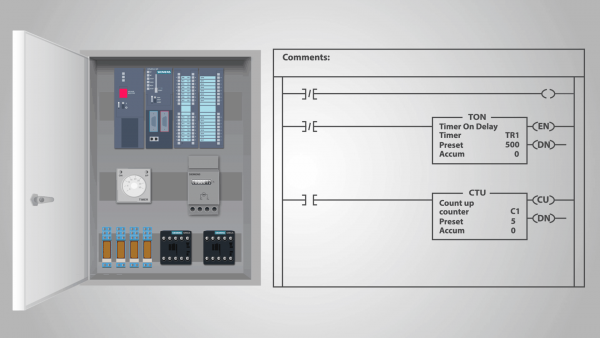
Un controlador lógico programable (PLC) es un ejemplo de un dispositivo de acción de relé que puede denominarse máquina de estado independiente.
De hecho, una vez que el programa se ha introducido en el PLC y el controlador ha comenzado a calcular, no está expuesto a influencias externas y cada estado posterior está completamente determinado por su estado anterior. Podemos suponer que la entrada tiene el mismo estado en cada ciclo de reloj.
Por el contrario, cualquier máquina de estados finitos que tiene el único estado de entrada posible se denomina naturalmente autónoma, ya que en este caso el entorno externo no lleva información que controle su comportamiento.
Ver también:
El uso de sistemas de microprocesador en ingeniería eléctrica en el ejemplo del uso de PLC.