Cálculo de potenciómetro y shunt compuesto

Conceptos y fórmulas

Un potenciómetro es una resistencia variable con un control deslizante que se incluye como se muestra en la fig.

Para obtener más detalles, consulte: Potenciómetros y sus aplicaciones.

Se aplica un voltaje U a los puntos 1 y 2. Se elimina un voltaje ajustable de los puntos 2 y 3, cuyo valor es menor que U y depende de la posición del control deslizante. Los divisores de voltaje tienen un esquema similar, pero no son ajustables y no tienen un control deslizante móvil.

Potenciómetros, divisores de voltaje y shunts complejos se calculan usando leyes de Kirchhoff, como el cálculo de circuitos convencionales con resistencias.

Ejemplos de

1. El voltaje de la fuente es U = 24 V, la resistencia total del potenciómetro es r = 300 Ohm. El motor se monta por separado para que r1 = 50 ohmios. ¿Qué voltaje U1 se puede quitar de los puntos 3 y 2 (Fig. 1)?

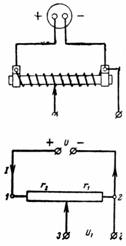
Arroz. 1.

La corriente I y el voltaje U a través de la resistencia r están relacionados por la fórmula I ∙ r = U.

El control deslizante del potenciómetro separa parte de la resistencia, es decir. la resistencia r1. La caída de tensión entre los puntos 3 y 2 es igual a I ∙ r1 = U1.

Del cociente de la caída de tensión se obtiene la igualdad (I ∙ r1) / (I ∙ r) = U1 / U. Cuanto mayor sea la resistencia r1, mayor será el valor de la tensión U1 entre los puntos 3 y 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. El potenciómetro (Fig. 2) se carga en una lámpara con resistencia r = 100 Ohm. El potenciómetro está dividido por un control deslizante en dos partes con r1 = 600 ohmios y r2 = 200 ohmios. Determine el voltaje Ul y la corriente de la lámpara Il.

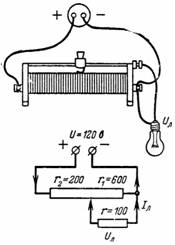
Arroz. 2.

La corriente I fluye a través de la resistencia r2 y la corriente Il fluye a través de la lámpara. Una corriente I-Il fluye a través de la resistencia r1, lo que crea un voltaje a través de la resistencia r1 igual al voltaje de la lámpara: (I-Il) ∙ r1 = Ul.

Por otro lado, el voltaje de la lámpara es igual al voltaje de la fuente menos caída de voltaje en la resistencia r2: U-I ∙ r2 = Ul.

La corriente I es igual al voltaje de la fuente dividido por la resistencia resultante de la conexión en serie-paralelo de las resistencias:

I = U / (r2 + (r ∙ r1) / (r + r1)).

Sustituimos la expresión por la corriente total de la fuente en la segunda ecuación:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Después de la transformación, obtenemos una expresión para el voltaje de la lámpara:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Si transformamos esta expresión, partiendo del hecho de que Ul = Il ∙ r, obtenemos una expresión para la corriente de la lámpara:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Sustituye los valores numéricos en las ecuaciones resultantes:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0,36 A.

3. Calcular la tensión Up y la corriente Ip del dispositivo de medida que está conectado a una parte del potenciómetro. El dispositivo tiene una resistencia de r = 1000 Ohm. El punto de bifurcación divide la resistencia del divisor en r2 = 500 ohmios y r1 = 7000 ohmios (Fig. 3).Tensión en los terminales del potenciómetro U = 220 V.

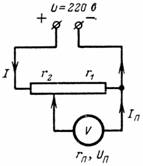
Arroz. 3.

Usando las fórmulas obtenidas anteriormente, podemos escribir que la corriente que fluye a través del dispositivo es:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14 A.

Arriba = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Calcular el voltaje del dispositivo Up, si consume una corriente Ip = 20 mA y está conectado a un potenciómetro dividido en resistencias r2 = 10 ^ 4 Ohm y r1 = 2 ∙ 10 ^ 4 Ohm (Fig. 3).

La tensión total en el divisor de tensión es igual a la suma de las caídas de tensión en sus partes (a través de las resistencias r1 y r2): U = I ∙ r2 + I1 ∙ r1; U = yo ∙ r2 + arriba

La fuente de corriente se ramifica en el punto de contacto del motor: I = I1 + Ip; I = Upn / r1 + In.

Sustituimos el valor de la corriente I en la ecuación de voltaje:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uï / r1 ∙ r2 + Iï ∙ r2 + Uï;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Por tanto, la tensión del dispositivo Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Sustituye los valores numéricos: Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Una fuente de corriente continua con tensión U = 120 V alimenta los circuitos anódicos del radiorreceptor a través de un potenciómetro (divisor de tensión), que junto con el filtro tiene una resistencia de r = 10000 Ohm. El voltaje U1 es eliminado por la resistencia r2 = 8000 Ohm. Calcule el voltaje del ánodo sin carga y con corriente de carga I = 0.02 A (Fig. 4).

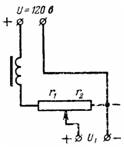
Arroz. 4.

El primer caso es similar al ejemplo 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

El segundo caso es similar al ejemplo 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Al cargar, el voltaje caerá de 96 a 64 V.Si se necesita más voltaje, entonces se debe mover el control deslizante hacia la izquierda, es decir, se debe aumentar la resistencia r2.

6. Los voltajes Ua y Ub son eliminados por el divisor de voltaje. La resistencia total del divisor de voltaje conectado al voltaje U1 = 220 V es r = 20,000 Ohm. ¿Cuál es el voltaje Ua en la resistencia r3 = 12000 Ohm con consumo de corriente Ia = 0.01 A y el voltaje Ub en la resistencia r2 + r3 = 18000 Ohm con consumo de corriente Ib = 0.02 A (Fig. 5).

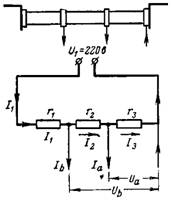
Arroz. 5.

Resistencia de voltaje r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

El voltaje Ub es igual a la suma de la caída de voltaje Ua en la resistencia r3 y la caída de voltaje en la resistencia r2. La caída de tensión en la resistencia r2 es igual a I2 ∙ r2. Corriente I2 = Ia + I3. La corriente I3 se puede calcular como en el ejemplo 1:

I3 = (220-80-40) / 20 000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Tensión Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

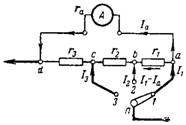
7. Calcular el shunt combinado para el miliamperímetro para que en diferentes posiciones del interruptor tenga los siguientes rangos de medida: I1 = 10 mA; I2 = 30mA; I3 = 100 mA. El diagrama de conexión de derivación se muestra en la fig. 6. Resistencia interna del dispositivo ra = 40 Ohm. Rango de medida intrínseco del miliamperímetro 2 mA.

Arroz. 6.

Al medir la corriente I≤2mA, la derivación se apaga.

a) Al medir la corriente I = 10 mA, el interruptor está en la posición 1 y fluye una corriente de 10-2 = 8 mA por todas las resistencias de derivación. La caída de tensión en la resistencia de derivación Ush y el dispositivo Ua entre los puntos d y a debe ser la misma

Ush = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Al medir la corriente I2 = 30 mA, el interruptor está en la posición 2. La corriente medida se dividirá en el punto b. En la desviación total del puntero del dispositivo, la corriente Ia = 2 mA pasará a través de la resistencia r1 y el dispositivo ra.

El resto de la corriente I2-Ia pasará por las resistencias r2 y r3. Las corrientes crearán la misma caída de voltaje en las dos ramas entre los puntos d y b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) De manera similar, realizaremos el cálculo al aumentar el rango de medida a I3 = 100 mA. La corriente I3-Ia fluirá a través de la resistencia r3 y la corriente Ia a través de las resistencias r1, r2, ra. La tensión en ambas ramas es la misma: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Obtuvimos tres ecuaciones con tres valores desconocidos de las resistencias r1, r2 y r3.

Multiplicamos todas las ecuaciones por 1000 y las convertimos:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Sumemos la primera y la tercera ecuación: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohmio.

Sumemos la primera y la segunda ecuación: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohmios.

Sustituyamos los resultados obtenidos en la primera ecuación: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohmios.

La exactitud del cálculo se puede verificar reemplazando los valores de resistencia obtenidos en las ecuaciones.