caída de tensión
Conceptos y fórmulas
En cada resistencia r, cuando pasa la corriente I, aparece un voltaje U = I ∙ r, que generalmente se denomina caída de voltaje de esta resistencia.
Si solo hay una resistencia r en el circuito, todo el voltaje de la fuente Ust cae sobre esta resistencia.
Si el circuito tiene dos resistencias r1 y r2 conectadas en serie, entonces la suma de los voltajes en las resistencias U1 = I ∙ r1 y U2 = I ∙ r2, es decir la caída de tensión es igual a la tensión de la fuente: Ust = U1 + U2.
La tensión de alimentación es igual a la suma de las caídas de tensión en el circuito (segunda ley de Kirchhoff).
Ejemplos de
1. ¿Qué caída de voltaje ocurre a través del filamento de la lámpara con resistencia r = 15 Ohm cuando pasa la corriente I = 0.3 A (Fig. 1)?
Arroz. 1.
El número de caídas de tensión Ley de Ohm: U = yo ∙ r = 0,3 ∙ 15 = 4,5 V.
La tensión entre los puntos 1 y 2 de la lámpara (ver esquema) es de 4,5 V. La lámpara se enciende normalmente si por ella circula corriente nominal o si entre los puntos 1 y 2 hay tensión nominal (la corriente nominal y la tensión se indican en la lámpara).
2. Dos bombillas idénticas para un voltaje de 2,5 V y una corriente de 0,3 A están conectadas en serie y conectadas a una batería de bolsillo con un voltaje de 4,5 V. ¿Qué caída de voltaje se genera en los terminales de las bombillas individuales? (Fig. 2 ) ) ?
Arroz. 2.
Bombillas idénticas tienen la misma resistencia r. Cuando se conectan en serie, por ellos circula la misma corriente I. Se deduce que tendrán las mismas caídas de tensión, la suma de estas tensiones debe ser igual a la tensión de la fuente U = 4,5 V. Cada bombilla tiene una tensión de 4 , 5: 2 = 2,25 V.
Puede resolver este problema y el cálculo secuencial. Calculamos la resistencia de la bombilla según los datos: rl = 2,5 / 0,3 = 8,33 ohmios.
Corriente del circuito I = U / (2rl) = 4,5 / 16,66 = 0,27 A.
La caída de tensión en la bombilla U = Irl = 0,27 ∙ 8,33 = 2,25 V.
3. El voltaje entre el riel y el cable de contacto de la línea del tranvía es de 500 V. Para la iluminación se utilizan cuatro lámparas idénticas conectadas en serie. ¿Para qué voltaje se debe seleccionar cada lámpara (Fig. 3)?
Arroz. 3.
Lámparas idénticas tienen resistencias iguales a través de las cuales fluye la misma corriente. La caída de tensión en las lámparas también será la misma. Esto significa que para cada lámpara habrá 500: 4 = 125 V.
4. Dos lámparas con una potencia de 40 y 60 W con un voltaje nominal de 220 V están conectadas en serie y están conectadas a una red con un voltaje de 220 V. ¿Qué caída de voltaje ocurre en cada uno de ellos (Fig. 4)?
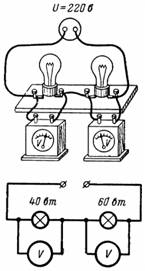
Arroz. 4.
La primera lámpara tiene una resistencia r1 = 1210 ohmios, y la segunda r2 = 806,6 ohmios (en estado calentado). La corriente que pasa por las lámparas es I = U / (r1 + r2) = 220 / 2016.6 = 0.109 A.
Caída de tensión en la primera lámpara U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.
Caída de tensión en la segunda lámpara U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.
Una lámpara con mayor resistencia tiene una mayor caída de voltaje y viceversa. Los filamentos de ambas lámparas son muy débiles, pero la lámpara de 40W es un poco más fuerte que la lámpara de 60W.
5. Para que el voltaje del motor eléctrico D (Fig. 5) sea igual a 220 V, el voltaje al comienzo de la línea larga (en la planta de energía) debe tener un valor superior a 220 V caída de voltaje (pérdida) en línea. Cuanto mayor sea la resistencia de la línea y la corriente en ella, mayor será la caída de voltaje a lo largo de la línea.
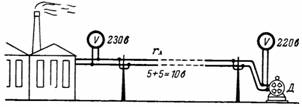Arroz. 5.
En nuestro ejemplo, la caída de voltaje en cada cable de la línea es de 5 V. Luego, el voltaje en las barras colectoras de la central eléctrica debe ser igual a 230 V.
6. El consumidor está alimentado por una batería de 80 V con una corriente de 30 A. Para el funcionamiento normal del consumidor, se permite una caída de voltaje del 3% en cables de aluminio con una sección transversal de 16 mm2. ¿Cuál es la distancia máxima de la batería al usuario?
Caída de tensión admisible en la línea U = 3/100 ∙ 80 = 2,4 V.
La resistencia de los cables está limitada por la caída de tensión permitida rpr = U / I = 2,4 / 30 = 0,08 ohmios.
Usando la fórmula para determinar la resistencia, calculamos la longitud de los cables: r = ρ ∙ l / S, de donde l = (r ∙ S) / ρ = (0.08 ∙ 16) / 0.029 = 44.1 m.
Si el usuario se encuentra a 22 m de la batería, la tensión en la misma será inferior a 80 V al 3%, es decir igual a 77,6 V.
7. Una línea de telégrafo de 20 km de largo está hecha de alambre de acero con un diámetro de 3,5 mm. Se sustituye la línea de retorno por puesta a tierra mediante barras metálicas. La resistencia de transición entre la barra y tierra es rz = 50 Ohm.¿Cuál debe ser el voltaje de la batería al principio de la línea si la resistencia del relé al final de la línea es rp = 300 Ohm y la corriente del relé es I = 5 mA?
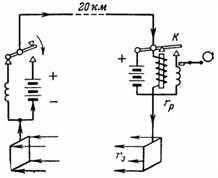
Arroz. 6.
El diagrama de conexión se muestra en la fig. 6. Cuando se presiona el interruptor del telégrafo en el punto de envío de la señal, el relé en el punto de recepción al final de la línea atrae la armadura K, que a su vez enciende la bobina de la grabadora con su contacto. La tensión de salida debe compensar la caída de tensión en la línea, el relé receptor y las resistencias transitorias de las barras de puesta a tierra: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = yo ∙ (rr + rr + 2 ∙ rr).
El voltaje de la fuente es igual al producto de la corriente y la resistencia total del circuito.
Sección transversal del cable S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.
Resistencia de línea rl = ρ ∙ l / S = 0,11 ∙ 20.000 / 9,6 = 229,2 ohmios.
Resistencia resultante r = 229,2 + 300 + 2 ∙ 50 = 629,2 ohmios.
Tensión de salida U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.
La caída de tensión en la línea durante el paso de una corriente I = 0,005 A será: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.
La caída de voltaje relativamente baja en la línea se logra debido al bajo valor de la corriente (5 mA). Por lo tanto, en el punto de recepción debe haber un relé sensible (amplificador), que se enciende con un pulso débil de 5 mA y, a través de su contacto, enciende otro relé más potente.
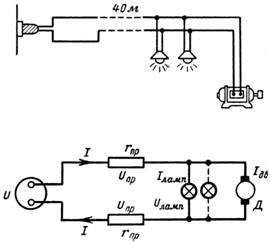
8. ¿Qué tan alto es el voltaje de las lámparas en el circuito de la fig. 28, cuando: a) el motor no está encendido; b) el motor arranca; c) el motor está en marcha.
El motor y 20 lámparas están conectados a una red eléctrica de 110 V. Las lámparas están diseñadas para 110 V y 40 W. La corriente de arranque del motor es Ip = 50 A y su corriente nominal es In = 30 A.
El alambre de cobre introducido tiene una sección transversal de 16 mm2 y una longitud de 40 m.
Higo. 7 y las condiciones del problema, se puede ver que la corriente del motor y de la lámpara hace que el voltaje de línea caiga, por lo tanto, el voltaje de carga será menor a 110V.
Arroz. 7.
U = 2 ∙ Ul + Ulámpara.
Por lo tanto, el voltaje en las lámparas Ulamp = U-2 ∙ Ul.
Es necesario determinar la caída de voltaje en la línea a diferentes corrientes: Ul = I ∙ rl.
Resistencia de toda la línea
2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 ohmios.
La corriente que pasa por todas las lámparas.
20 ∙ Ilámpara = 20 ∙ 40/110 = 7,27 A.
Caída de voltaje de la red cuando solo las lámparas están encendidas (sin motor),
2 ∙ Ul = Ilámpara ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.
El voltaje en las lámparas en este caso es:
Ulámpara = U-2 ∙ Ul = 110-0,65 = 109,35 V.
Al arrancar el motor, las lámparas brillarán más tenuemente, ya que la caída de tensión en la línea es mayor:
2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.
La tensión mínima de las lámparas al arrancar el motor será:
Ulámpara = Uc-2, Ul = 110-5,1 = 104,9 V.
Cuando el motor está en marcha, la caída de voltaje en la línea es menor que cuando el motor arranca, pero mayor que cuando el motor está apagado:
2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.
El voltaje de las lámparas durante el funcionamiento normal del motor es:
Ulámpara = 110-3,32 = 106,68 V.
Incluso una ligera disminución en el voltaje de las lámparas en relación con el nominal afecta significativamente el brillo de la iluminación.