Rigidez dieléctrica del aislamiento. Ejemplos de cálculo

Con un aumento gradual en el voltaje U entre conductores separados por un dieléctrico (aislamiento), por ejemplo, placas de capacitores o cables conductores, la intensidad (fuerza) del campo eléctrico en el dieléctrico aumenta. La fuerza del campo eléctrico en el dieléctrico también aumenta a medida que disminuye la distancia entre los cables.

A cierta intensidad de campo, se produce una ruptura en el dieléctrico, se forma una chispa o un arco y aparece una corriente eléctrica en el circuito. La intensidad del campo eléctrico a la que se produce la ruptura del aislamiento se denomina intensidad eléctrica Epr del aislamiento.

La rigidez dieléctrica se define como el voltaje por mm de espesor de aislamiento y se mide en V/mm (kV/mm) o kV/cm. Por ejemplo, la rigidez dieléctrica del aire entre placas lisas es de 32 kV/cm.

La fuerza del campo eléctrico en un dieléctrico para el caso en que los conductores están en forma de placas o tiras separadas por un espacio igual (por ejemplo, en un capacitor de papel) se calcula mediante la fórmula

E = U / d,

donde U es el voltaje entre los cables, V (kV); d — espesor de la capa dieléctrica, mm (cm).

Ejemplos de

1. ¿Cuál es la intensidad del campo eléctrico en el entrehierro de 3 cm de espesor entre las placas si la tensión entre ellas es U = 100 kV (Fig. 1)?

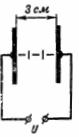
Arroz. 1.

La intensidad del campo eléctrico es: E = U / d = 100000/3 = 33333 V / cm.

Tal tensión supera la rigidez dieléctrica del aire (32 kV/cm) y existe riesgo de destrucción.

El riesgo de daños por CC puede evitarse aumentando el espacio, por ejemplo, a 5 cm, o utilizando otro aislamiento más fuerte en lugar de aire, como cartón eléctrico (Fig. 2).

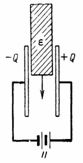
Arroz. 2.

El cartón eléctrico tiene una constante dieléctrica de ε = 2 y una rigidez dieléctrica de 80 000 V/cm. En nuestro caso, la intensidad del campo eléctrico en el aislamiento es de 33333 V. El aire no puede soportar esta fuerza, mientras que el cartón eléctrico en este caso tiene una reserva de rigidez dieléctrica de 80.000/33333 = 2,4, ya que la rigidez dieléctrica del cuadro eléctrico es 80.000/32.000 = 2,5 veces la del aire.

2. ¿Cuál es la intensidad del campo eléctrico en el dieléctrico de un capacitor de 3 mm de espesor si el capacitor está conectado a un voltaje U = 6 kV?

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Un dieléctrico de 2 mm de espesor se rompe a una tensión de 30 kV. ¿Cuál era su fuerza eléctrica?

E = U / d = 30.000 / 0,2 = 150.000 V / cm = 150 kV / cm. El vidrio tiene tal fuerza eléctrica.

4. El espacio entre las placas del condensador se rellena con capas de cartón eléctrico y una capa de mica del mismo espesor (Fig. 3). El voltaje entre las placas del capacitor es U = 10000 V. El cartón eléctrico tiene una constante dieléctrica ε1 = 2 y mica ε2 = 8.¿Cómo se distribuirá el voltaje U entre las capas de aislamiento y qué intensidad tendrá el campo eléctrico en las capas individuales?

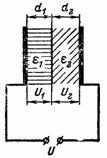
Arroz. 3.

Los voltajes U1 y U2 a través de capas dieléctricas del mismo espesor no serán iguales. La tensión del condensador se dividirá en tensiones U1 y U2, que serán inversamente proporcionales a las constantes dieléctricas:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Como U = U1 + U2, tenemos dos ecuaciones con dos incógnitas.

Sustituye la primera ecuación en la segunda: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Por tanto, 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000V.

Aunque las capas dieléctricas tienen el mismo grosor, no tienen la misma carga. Un dieléctrico con una constante dieléctrica más alta está menos cargado (U2 = 2000 V) y viceversa (U1 = 8000 V).

La intensidad del campo eléctrico E en las capas dieléctricas es igual a:

E1 = U1 / d1 = 8000 / 0,2 = 40.000 V / cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

La diferencia en la constante dieléctrica conduce a un aumento en la fuerza del campo eléctrico. Si todo el espacio se llenara con un solo dieléctrico, por ejemplo, mica o cartón eléctrico, la intensidad del campo eléctrico sería menor, ya que se distribuiría de manera bastante uniforme en el espacio:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

Por lo tanto, es necesario evitar el uso de aislamientos complejos con constantes dieléctricas muy diferentes. Por la misma razón, el riesgo de falla aumenta cuando se forman burbujas de aire en el aislamiento.

5. Determine la fuerza del campo eléctrico en el dieléctrico del capacitor del ejemplo anterior si el grosor de las capas dieléctricas no es el mismo.El tablero eléctrico tiene un espesor d1 = 0,2 mm y mica d2 = 3,8 mm (Fig. 4).

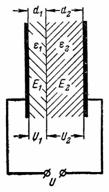
Arroz. 4.

La intensidad del campo eléctrico se distribuirá inversamente proporcional a las constantes dieléctricas:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Como E1 = U1 / d1 = U1 / 0.2 y E2 = U2 / d2 = U2 / 3.8, entonces E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2.

Por lo tanto E1 / E2 = 4 = 19 ∙ U1 / U2, o U1 / U2 = 4/19.

La suma de los voltajes U1 y U2 en las capas dieléctricas es igual al voltaje de la fuente U: U = U1 + U2; 10000 = U1 + U2.

Como U1 = 4/19 ∙ U2, entonces 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190 000 /23 = 8260 V; U1 = U-U2 = 1740V.

La fuerza del campo eléctrico en la mica es E2 ∙ 8260 / 3.8≈2174 V / cm.

La mica tiene una fuerza eléctrica de 80.000 V/mm y puede soportar tal voltaje.

La intensidad del campo eléctrico en el cartón eléctrico es E1 = 1740 / 0,2 = 8700 V / mm.

El cartón eléctrico no resistirá tal voltaje, ya que su rigidez dieléctrica es de solo 8000 V / mm.

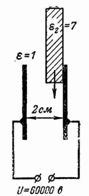
6. Se conecta un voltaje de 60 000 V a dos placas de metal separadas 2 cm. Determine la intensidad del campo eléctrico en el espacio de aire, así como la intensidad del campo eléctrico en el aire y el vidrio, si hay vidrio en el espacio, inserte una placa con un espesor de 1 cm (Fig. 5).

Arroz. 5.

Si solo hay aire entre las placas, la intensidad del campo eléctrico en él es igual a: E = U / d = 60,000 /2 = 30,000 V / cm.

La fuerza del campo está cerca de la fuerza dieléctrica del aire.Si se introduce en el hueco una placa de vidrio de 1 cm de espesor (constante dieléctrica de vidrio ε2 = 7), entonces E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60.000-U2; 8 ∙ U2 = 60.000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

La fuerza del campo eléctrico en el vidrio es E2 = 7,5 kV/cm, y su fuerza eléctrica es de 150 kV/cm.

En este caso, el vidrio tiene un factor de seguridad de 20 veces.

Para el entrehierro tenemos: U1 = 60.000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

En este caso, la fuerza del campo eléctrico en el entrehierro es mayor que en el primero, sin vidrio. Después de insertar el vidrio, toda la combinación tiene menos fuerza que el aire solo.

El riesgo de rotura también se produce cuando el grosor de la placa de vidrio es igual al espacio entre las placas conductoras, es decir 2 cm, ya que inevitablemente habrá pequeños espacios de aire en el espacio que se perforará.

La rigidez dieléctrica del hueco entre los conductores de alta tensión debe reforzarse con materiales que tengan una constante dieléctrica baja y una rigidez dieléctrica alta, por ejemplo, cartón eléctrico con ε = 2. Evitar combinaciones de materiales con una constante dieléctrica alta (vidrio , porcelana) y aire, que debe ser reemplazado con aceite.