Cálculo de la capacitancia del capacitor
 La capacitancia C es la capacidad del capacitor para aceptar (almacenar y retener) la cantidad de electricidad Q en amperios-segundo o la carga Q en colgantes. Si le dices a un cuerpo, por ejemplo una pelota, una carga eléctrica (cantidad de electricidad) Q, entonces un electroscopio conectado entre este cuerpo y el suelo mostrará un voltaje U (Fig. 1). Este voltaje es proporcional a la carga y también depende de la forma y tamaño del cuerpo.
La capacitancia C es la capacidad del capacitor para aceptar (almacenar y retener) la cantidad de electricidad Q en amperios-segundo o la carga Q en colgantes. Si le dices a un cuerpo, por ejemplo una pelota, una carga eléctrica (cantidad de electricidad) Q, entonces un electroscopio conectado entre este cuerpo y el suelo mostrará un voltaje U (Fig. 1). Este voltaje es proporcional a la carga y también depende de la forma y tamaño del cuerpo.
La relación entre la carga Q y el voltaje U se expresa mediante la fórmula Q = C ∙ U.
La constante de proporcionalidad C se llama capacitancia del cuerpo. Si el cuerpo tiene forma de bola, la capacitancia del cuerpo es proporcional al radio de la bola r.
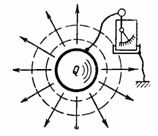
Arroz. 1.
La unidad de medida de la capacitancia es el faradio (F).
El cuerpo tiene una capacitancia de 1 F cuando una carga de 1 k produce un voltaje de 1 V entre él y tierra. Los faradios son una unidad de medida muy grande, por lo que en la práctica se utilizan unidades más pequeñas: microfaradio (μF), nanofaradio (nF) y picofaradio (pF)...
Estas unidades están relacionadas por las siguientes proporciones: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.
La capacitancia de una bola con un radio de 1 cm es 1.1 pF.
No solo un cuerpo aislado puede acumular carga, sino también un dispositivo especial llamado capacitor. Un condensador consta de dos o más placas (placas) que están separadas por un dieléctrico (aislamiento).
En la Fig. 2 muestra un circuito con una fuente de CC conectada a un condensador. Cuando se enciende, se forma una carga positiva +Q en la placa derecha del capacitor y una carga negativa -Q en la placa izquierda. Durante carga del condensador una corriente fluye a través del circuito, que se detiene después del final de la carga; entonces el voltaje a través del capacitor será igual a e. etc. c. fuente U. La carga en la placa del capacitor, el voltaje y la capacitancia están relacionados por la relación Q = C ∙ U. En este caso, se forma un campo electrostático en el dieléctrico del capacitor.
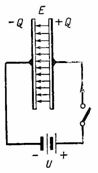
Arroz. 2.
La capacidad de un capacitor con un dieléctrico de aire se puede calcular mediante la fórmula C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, donde S es el área de una placa, cm2; d es la distancia entre las placas, cm; C es la capacitancia del capacitor, pF.
La capacidad de un capacitor que consta de n placas (Fig. 3) es igual a: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.
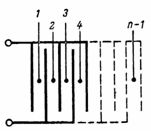
Arroz. 3.
Si el espacio entre las placas se llena con otro dieléctrico, por ejemplo papel, la capacitancia del capacitor aumentará en un factor de ε. Cuando se usa aislamiento de papel, la capacidad aumentará 3 veces, con aislamiento de mica, de 5 a 8 veces, con vidrio, 7 veces, etc. El valor de ε se denomina constante dieléctrica del dieléctrico.
La fórmula general para determinar la capacitancia de un capacitor con constante dieléctrica ε (épsilon) es: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.
Esta fórmula es útil para calcular pequeños condensadores variables para radios.La misma fórmula se puede representar como: C = (ε_0 ∙ ε ∙ S) / d, donde ε_0 es la constante dieléctrica o la constante dieléctrica del vacío (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε es la constante dieléctrica del dieléctrico.
En esta fórmula, las dimensiones se reemplazan en metros y la capacitancia se obtiene en faradios.
Ejemplos de
1. ¿Cuál es la capacidad del planeta Tierra, cuyo radio es r = 6378 km?
Dado que la capacitancia de una esfera de 1 cm de radio es igual a 1,11 pF, la capacitancia de la Tierra es: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (La capacidad de una bola del tamaño de nuestro planeta es relativamente pequeña. Los capacitores electrolíticos de tamaño pequeño tienen esta capacidad).
2. Determine la capacitancia de un capacitor que consta de dos placas, cada una de las cuales tiene un área S = 120 cm2.
Las placas están separadas por una capa de aire con un espesor de d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF .. .
3. Determinar la capacitancia del capacitor con los datos dados en el ejemplo anterior, si el espacio entre las placas se llena con papel encerado con constante dieléctrica ε = 4, vidrio (ε = 7), cartón eléctrico (ε = 2) , mica (ε = 8 ).
Un capacitor de papel encerado tiene una capacitancia C = ε ∙ (S ∙ 1.11) / (4 ∙ π ∙ d) = 4 ∙ 21.2 = 84.8 pF.
La capacitancia de un capacitor de vidrio es C = 7 ∙ 21.2 = 148.4 pF.
La capacitancia del capacitor de cartón es C = 2 ∙ 21.2 = 42.3 pF.
La capacitancia del capacitor de mica es C = 8 ∙ 21.2 = 169.6 pF.
4. ¿Cuál es la capacitancia de un condensador rotatorio de aire para un receptor de radio que consta de 20 placas con un área de 20 cm2 si la distancia entre las placas es de 0,06 cm (Fig. 149)?
C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.
El condensador que se muestra en la Fig.3, consta de capacitores más simples separados con dos placas, cuyo número es igual a n-1.
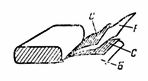
5. Un capacitor de papel de capacitancia C = 2 μF consta de dos tiras de papel de aluminio C y dos tiras de un dieléctrico hecho de papel encerado B con una constante dieléctrica ε = 6. El grosor del papel encerado es d = 0,1 mm. Las tiras plegadas se enrollan, los cables están hechos de placas de acero. Determine la longitud de la tira de acero del condensador si su ancho es de 4 cm (Fig. 4).
Arroz. 4.
Primero, determinamos el área de una tira por la fórmula C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, de donde S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.
La longitud de cada tira es l = 37680/4 = 9420 cm = 94,2 m.