Fuerza de tracción de electroimanes

La fuerza con la que un electroimán atrae los materiales ferromagnéticos depende del flujo magnético F o, de manera equivalente, de la inducción B y del área de la sección transversal del electroimán S.

La fuerza de presión del electroimán está determinada por la fórmula

F = 40550 ∙ segundo ^ 2 ∙ S,

donde F es la fuerza de presión del electroimán, kg (la fuerza también se mide en newtons, 1 kg = 9,81 N o 1 N = 0,102 kg); B — inducción, T; S es el área de la sección transversal del electroimán, m2.

Ejemplos de

1. El electroimán del grifo es un circuito magnético (Fig. 1). ¿Cuál es la fuerza de elevación del electroimán de una grúa de herradura, si la inducción magnética es B = 1 T, y el área de la sección transversal de cada polo del electroimán es S = 0,02 m2 (Fig. 1, b)? Desprecie el efecto del espacio entre el electroimán y la armadura.

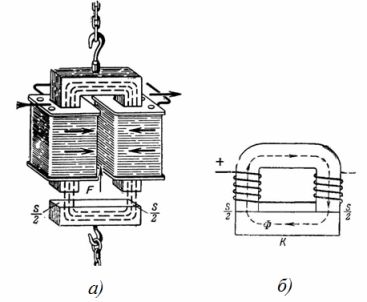
Arroz. 1. Electroimán de elevación

F = 40550 ∙ segundo ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

2. Un electroimán circular de acero tiene las dimensiones que se muestran en la fig. 2, a y b. La fuerza de elevación del electroimán es de 3 T. Determine el área de la sección transversal del núcleo del electroimán, n. p. y el número de vueltas de la bobina a una corriente de magnetización I = 0,5 A.

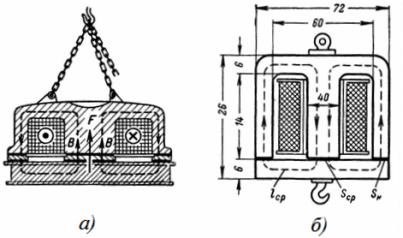
Arroz. 2. Electroimán redondo

El flujo magnético pasa a través del núcleo interno circular y regresa a través del cuerpo cilíndrico. Las áreas de la sección transversal del núcleo Sc y la carcasa Sk son aproximadamente iguales, por lo que los valores de inducción en el núcleo y la carcasa son prácticamente iguales:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

La inducción requerida en el electroimán está determinada por la fórmula F = 40550 ∙ B ^ 2 ∙ S,

donde B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

El voltaje en esta inducción se encuentra en la curva de magnetización del acero fundido:

H = 180 A/m.

La longitud promedio de la línea de campo (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Fuerza de magnetización I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; yo = (yo ∙ ω) / yo = 154,8 / 0,5 = 310 A.

En realidad n. s, es decir, la corriente y el número de vueltas, deben ser muchas veces mayores, ya que entre el electroimán y la armadura hay un espacio de aire inevitable, lo que aumenta significativamente la resistencia magnética del circuito magnético. Por lo tanto, el entrehierro debe tenerse en cuenta al calcular los electroimanes.

3. La bobina del electroimán para el grifo tiene 1350 vueltas, a través de ella fluye una corriente I = 12 A. Las dimensiones del electroimán se muestran en la fig. 3. ¿Qué peso levanta el electroimán a una distancia de 1 cm de la armadura y qué peso puede soportar después de la gravedad?

Arroz. 3. Bobina electromagnética

La mayor parte de N. con I ∙ ω se gasta en conducir flujo magnético a través del entrehierro: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Fuerza de magnetización I ∙ ω = 12 ∙ 1350 = 16200 A.

Como H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, entonces Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02.

Por lo tanto, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02, es decir B = 1.012T.

Suponemos que la inducción es B = 1 T, ya que parte de n. c) I ∙ ω se gasta en conducir el flujo magnético en el acero.

Verifiquemos este cálculo con la fórmula I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

La longitud media de la línea magnética es: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

La intensidad Hc en B = 1 T (10000 Gs) se determina a partir de la curva de magnetización:

Hc = 260 A/m I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

La fuerza de magnetización I ∙ ω = 16114 Av que crea una inducción B = 1 T es prácticamente igual a la n dada. v. yo ∙ ω = 16200 av.

El área transversal total del núcleo y el cono es: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

El electroimán atraerá una carga de peso F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg desde una distancia de 1 cm.

Dado que el entrehierro prácticamente desaparece después de atraer la armadura, el electroimán puede soportar una carga mucho mayor. En este caso, todo el n. c) I ∙ ω se gasta en conducir flujo magnético solo en acero, por lo tanto I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

A tal voltaje, el acero está prácticamente saturado y la inducción en él es de aproximadamente 2 T. El electroimán atrae la armadura con una fuerza F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0.006 = 973 kg.

4. El relé de señal (intermitente) consiste en un electroimán blindado 1 con un núcleo redondo y una armadura tipo válvula 2 que, después de suministrar corriente al electroimán, atrae y libera el intermitente 3, que abre el dígito de la señal (Fig. 4).

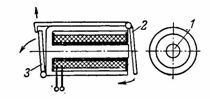
Arroz. 4. Electroimán de armadura

La fuerza de magnetización es I ∙ ω = 120 Av, el espacio de aire es δ = 0,1 cm y el área transversal total del electroimán es S = 2 cm2. Estime la fuerza de tracción del relé.

La inductancia B se determina mediante aproximaciones sucesivas utilizando la ecuación I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Sea n. c. Hc ∙ lc es 15% I ∙ ω, es decir Av. 18

Entonces yo ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Por lo tanto, encontramos la inducción B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Después de sustituir el valor B en la fórmula F = 40550 ∙ B ^ 2 ∙ S, obtenemos:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

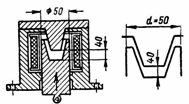
5. El solenoide del freno de CC (Fig. 5) tiene una armadura de pistón con un tope cónico. La distancia entre la armadura y el núcleo es de 4 cm El diámetro de trabajo (núcleos con un área de contacto circular) d = 50 mm. La armadura se introduce en la bobina con una fuerza de 50 kg. La longitud de la línea media de fuerza lav = 40 cm Determine n. pp. y la corriente de la bobina si son 3000 vueltas.

Arroz. 5. Solenoide de freno de CC

El área de la sección de trabajo del electroimán es igual al área de un círculo con un diámetro d = 5 cm:

S = (π ∙ re ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

La inducción B requerida para crear una fuerza F = 50 kg se encuentra a partir de la ecuación F = 40550 ∙ B ^ 2 ∙ S,

donde B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Fuerza de magnetización I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Determinamos la fuerza magnetizante para el acero Hc ∙ lc de forma simplificada, basándonos en que es del 15% I ∙ ω:

yo ∙ ω = 0.15 ∙ yo ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ yo ∙ ω = 8 ∙ 10 ^ 5 ∙ segundo ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Av.

Corriente de magnetización I = (I ∙ ω) / ω = 30000/3000 = 10 A.