Cálculo de la potencia de corriente trifásica.
En el artículo, para simplificar la notación, los valores lineales de voltaje, corriente y potencia de un sistema trifásico se darán sin subíndices, es decir U, I y P.
La potencia de una corriente trifásica es igual a tres veces la potencia de una sola fase.
Cuando está conectado en estrella PY = 3 Uph Iphcosfi = 3 Uph Icosfie.
Cuando está conectado por un triángulo P = 3 Uph Iphcosfi= 3 U Iphcosfie.
En la práctica, se usa una fórmula en la que la corriente y el voltaje significan cantidades lineales para conexiones tanto en estrella como en triángulo. En la primera ecuación sustituimos Uph = U / 1.73, y en la segunda Iph = I / 1.73 obtenemos la fórmula general P =1, 73 U Icosfie.
Ejemplos de
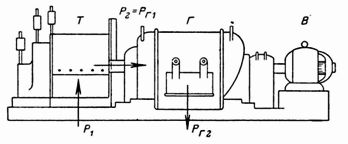
1. ¿Qué potencia P1 recibe de la red el motor de inducción trifásico que se muestra en la fig. 1 y 2 cuando se conectan en estrella y triángulo si la tensión de línea U = 380 V y la corriente de línea I = 20 A con cosfie=0,7 ·
El voltímetro y el amperímetro muestran valores lineales, valores medios.
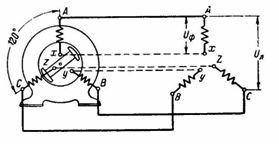
Arroz. 1.
Arroz. 2.
La potencia del motor según la fórmula general será:
P1 = 1,73 U Icosfie=1,73·380 20 0,7 = 9203 W = 9,2 kW.
Si calculamos la potencia por los valores de fase de corriente y voltaje, entonces cuando se conecta a una estrella, la corriente de fase es If = I = 20 A, y el voltaje de fase Uf = U / 1.73 = 380 / 1.73,
de ahí el poder
P1 = 3 Uph Iphcosfie= 3 U / 1,73 Icosfie=31,7380/1,73·20·0,7;
P1 = 3·380 / 1,73 20 0,7 = 9225 W = 9,2 kW.
Cuando se conecta en un triángulo, el voltaje de fase Uph = U y la corriente de fase Iph = I /1.73=20/1, 73; de este modo,
P1 = 3 Uph Iphcosfie= 3 UI /1.73·cosfie;
P1 = 3·380 20 / 1,73 0,7 = 9225 W = 9,2 kW.
2. Las lámparas están conectadas a la red de corriente trifásica de cuatro hilos entre la línea y los cables neutros, y el motor D está conectado a los tres cables de línea, como se muestra en la fig. 3.
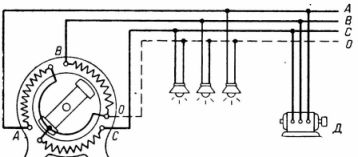
Arroz. 3.
Cada fase incluye 100 lámparas de 40 W cada una y 10 motores con una potencia de 5 kW. ¿Qué potencia activa y total debe dar el generador G en senfi = 0.8 Cuáles son las corrientes de fase, línea y neutro del generador a un voltaje U = 380 V
La potencia total de las lámparas es Pl = 3 100 40 W = 12 000 W = 12 kW.
Las lámparas están bajo tensión de fase Uf = U /1, 73 = 380 / 1,73 = 220 V.
La potencia total de los motores trifásicos Pd = 10 5 kW = 50 kW.
La potencia activa entregada por el generador, PG, y recibida por el consumidor P1 es igual, si ignoramos la pérdida de potencia en los cables de transmisión:
P1 = PG = Pl + Pd = 12 + 50 = 62 kW.
Potencia aparente del generador S = PG /cosfie = 62 / 0,8 = 77,5 kVA.
En este ejemplo, todas las fases tienen la misma carga y, por lo tanto, la corriente en el cable neutro en cualquier instante es cero.
La corriente de fase del devanado del estator del generador es igual a la corriente de línea (Iph = I) y su valor se puede obtener mediante la fórmula para la potencia de la corriente trifásica:
I = P / (1.73Ucosfie) = 62000 / (1.73 380 0.8) = 117.8 A.
3. En la fig.4 muestra que una placa de 500 W está conectada a la fase B y al cable neutro, y una lámpara de 60 W está conectada a la fase C y al cable neutro. Las tres fases ABC están conectadas a un motor de 2 kW a cosfie= 0,7 y una estufa eléctrica de 3 kW.
¿Cuál es la potencia activa y aparente total de los consumidores? ¿Qué corrientes pasan a través de las fases individuales a una tensión de red U = 380 V?
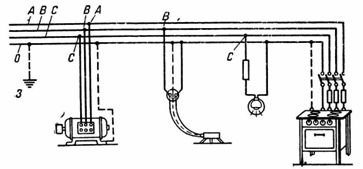
Arroz. 4.
Potencia activa de los consumidores P = 500 + 60 + 2000 + 3000 = 5560 W = 5,56 kW.
Potencia total del motor S = P /cosfie = 2000 / 0,7 = 2857 VA.
La potencia aparente total de los consumidores será: Stot = 500 + 60 + 2857 + 3000 = 6417 VA = 6.417 kVA.
Corriente estufa eléctrica Ip = Pp / Uf = Pp / (U1, 73) = 500/220 = 2,27 A.
Corriente de lámpara Il = Pl / Ul = 60/220 = 0,27 A.
La corriente de la estufa eléctrica está determinada por la fórmula de potencia para corriente trifásica a cosfie= 1 (resistencia activa):
P =1, 73 U Icosfie=1, 73 * U * I;
I = P / (1,73 U) = 3000 / (1,73·380) = 4,56 A.
ID de corriente del motor = P / (1.73Ucosfie)=2000/(1.73380 0.7) = 4.34A.
El conductor de la fase A lleva corriente desde el motor y la estufa eléctrica:
IA = DI + I = 4,34 + 4,56 = 8,9 A.
En la fase B, la corriente fluye desde el motor, la placa y la estufa eléctrica:
IB = ID + Ip + I = 4,34 + 2,27 + 4,56 = 11,17 A.
En la fase C fluye corriente desde el motor, la lámpara y la estufa eléctrica:
IC = ID + Il + I = 4,34 + 0,27 + 4,56 = 9,17 A.
Las corrientes RMS se dan en todas partes.
En la Fig. 4 muestra la conexión a tierra de protección 3 de la instalación eléctrica. El cable neutro está conectado a tierra firmemente a la subestación de energía y al consumidor. Todas las partes de las instalaciones que pueden ser tocadas por una persona están conectadas al cable neutro y, por lo tanto, están puestas a tierra.
Si una de las fases se pone a tierra accidentalmente, por ejemplo C, se produce un cortocircuito monofásico y un fusible o disyuntor para esa fase la desconecta de la fuente de alimentación. Si una persona de pie en el suelo toca un cable sin aislar de las fases A y B, estará bajo tensión de fase solamente. Con un neutro sin puesta a tierra, la fase C no se desconectará y la cara se energizará con respecto a las fases A y B.
4. La potencia suministrada al motor se indicará mediante un vatímetro trifásico conectado a una red trifásica con tensión de línea U = 380 V, corriente de línea I = 10 A y cosfie= 0,7 · K. p. D. Sobre el motor = 0,8 ¿Cuál es la potencia del motor sobre el eje (Fig. 5) ·
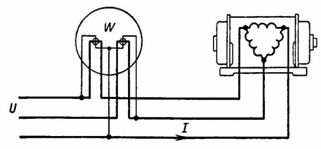
Arroz. 5.
El vatímetro mostrará la potencia suministrada al motor P1, es decir. la potencia neta P2 más la pérdida de potencia en el motor:
P1 =1,73U Icosfie=1,73·380 10 0,7 = 4,6 kW.
Potencia neta menos pérdidas de bobina y acero y pérdidas mecánicas en los rodamientos
P2 = 4,6 0,8 = 3,68 kW.
5. Un generador trifásico suministra corriente I = 50 A con tensión U = 400 V y cosfie = 0,7. ¿Qué potencia mecánica en caballos de fuerza se requiere para hacer girar el generador cuando la eficiencia del generador es 0.8 (Fig. 6)?
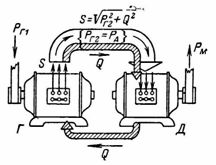
Arroz. 6.
Potencia eléctrica activa del generador entregada al motor eléctrico, PG2 = (3) U Icosfie= 1.73 400 50 0.7 = 24 220 W = 24.22 kW.
La potencia mecánica suministrada al generador, PG1, cubre la potencia activa de PG2 y sus pérdidas: PG1 = PG2 / G = 24,22 / 0,8·30,3 kW.
Esta potencia mecánica, expresada en caballos de fuerza, es:
PG1 = 30,3 * 1,36 * 41,2 litros. con
En la Fig. 6 muestra que la potencia mecánica PG1 se suministra al generador. El generador lo convierte en eléctrico, que es igual a
Esta potencia, activa e igual a PG2 = 1,73 U Icosfie, se transmite por cables a un motor eléctrico, donde se convierte en potencia mecánica.Además, el generador envía potencia reactiva Q al motor eléctrico, que magnetiza el motor, pero no se consume en él, sino que se devuelve al generador.
Es igual a Q = 1,73 · U · I · sinfi y no se convierte en energía térmica ni mecánica. La potencia aparente S = Pcosfie, como vimos antes, sólo determina el grado de aprovechamiento de los materiales consumidos en la fabricación de la máquina.]
6. Un generador trifásico opera con voltaje U = 5000 V y corriente I = 200 A con cosfie = 0.8. ¿Cuál es su eficiencia si la potencia que entrega el motor que hace girar al generador es de 2000 hp? con
Potencia del motor aplicada al eje del generador (si no hay engranajes intermedios),
PG1 = 2000 0,736 = 1473 kW.
La potencia desarrollada por un generador trifásico es
PG2 = (3) U Icosfie= 1,73 5000 200 0,8 = 1384000 W = 1384 kW.
Eficiencia del generador PG2 / PG1 = 1384/1472 = 0,94 = 94%.
7. ¿Qué corriente circula por el devanado de un transformador trifásico de 100 kVA de potencia y tensión U = 22000 V con cosfie=1
Potencia aparente del transformador S = 1,73 U I = 1,73 22000 I.
Por tanto, la corriente I = S/(1,73 U) = (100 1000)/(1,73 22000) = 2,63 A.;
8. ¿Cuál es la corriente consumida por un motor de inducción trifásico con una potencia de eje de 40 litros? con un voltaje de 380 V, si su cosfie = 0.8, y la eficiencia = 0.9
Potencia del motor en el eje, es decir útil, P2 = 40736 = 29440 W.
La potencia suministrada al motor, es decir, la potencia recibida de la red,
P1 = 29440 / 0,9 = 32711W.
Corriente del motor I = P1 / (1,73 U Icosfie)=32711/(1,73·380 0,8) = 62 A.
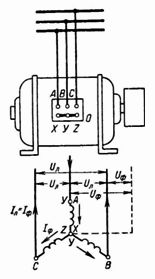
9. Un motor de inducción trifásico tiene los siguientes datos en el panel: P = 15 hp. con .; U = 380/220 V, cosfie= 0,8 conexión — estrella. Los valores indicados en la placa se denominan nominales.
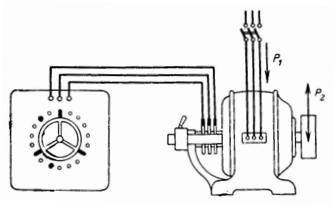
Arroz. 7.
¿Cuáles son las fuerzas activa, aparente y reactiva del motor? ¿Cuáles son las corrientes: completa, activa y reactiva (Fig. 7)?
La potencia mecánica del motor (red) es:
P2 = 15 0,736 = 11,04 kW.
La potencia suministrada P1 al motor es mayor que la potencia útil por la cantidad de pérdidas en el motor:
P1 = 11,04 / 0,85 13 kW.
Potencia aparente S = P1 /cosfie = 13 / 0,8 = 16,25 kVA;
Q = S sinfi = 16,25 0,6 = 9,75 kvar (ver triángulo de potencia).
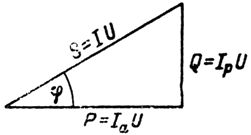
La corriente en los cables de conexión, es decir, lineal, es igual a: I = P1 / (1,73 Ucosfie) = S / (1,73 U) = 16250 / (1,731,7380) = 24,7 A.
Corriente activa Ia = Icosfie= 24,7 0,8 = 19,76 A.
Corriente reactiva (magnetizante) Ip = I sinfi = 24,7 0,6 = 14,82 A.
10. Determine la corriente en el devanado de un motor eléctrico trifásico si está conectado en triángulo y la potencia neta del motor P2 = 5.8 litros. con eficiencia = 90%, factor de potencia cosfie = 0,8 y tensión de red 380 V.
Potencia neta del motor P2 = 5,8 hp. seg., o 4,26 kW. Potencia al motor
P1 = 4,26 / 0,9 = 4,74 kW. I = P1 / (1,73 Ucosfie)=(4,74·1000)/(1,73·380 0,8) = 9,02 A.
Cuando se conecta en triángulo, la corriente en el devanado de fase del motor será menor que la corriente en los cables de alimentación: If = I / 1,73 = 9,02 / 1,73 = 5,2 A.
11. Un generador de CC para una planta de electrólisis, diseñado para voltaje U = 6 V y corriente I = 3000 A, en conexión con un motor asíncrono trifásico forma un generador de motor. La eficiencia del generador es G = 70%, la eficiencia del motor es D = 90% y el factor de potencia ecosfie = 0,8. Determine la potencia del motor del eje y la fuente de alimentación (Fig. 8 y 6).

Arroz. ocho.
Potencia neta del generador PG2 = UG · IG = 61,73000 = 18000 W.
La potencia suministrada al generador es igual a la potencia en el eje P2 del motor de inducción de accionamiento, que es igual a la suma de PG2 y las pérdidas de potencia en el generador, es decir, PG1 = 18000 / 0,7 = 25714 W.
La potencia activa del motor que se le suministra desde la red de CA,
P1 = 25714 / 0,9 = 28571 W = 28,67 kW.
12. Una turbina de vapor con eficiencia · T = 30% hace girar el generador con eficiencia = 92% y cosfie= 0.9. Que potencia de entrada (hp y kcal/s) debe tener la turbina para que el generador suministre una corriente de 2000 A a una tensión de U = 6000 V (Antes de iniciar el cálculo, ver Fig. 6 y 9).
Arroz. nueve.
La potencia del alternador suministrada al consumidor es
PG2 = 1,73·U Icosfie= 1,73 6000 2000 0,9 = 18684 kW.
La potencia suministrada por el generador es igual a la potencia P2 del eje de la turbina:
PG1 = 18684 / 0,92 = 20308 kW.
La energía es suministrada a la turbina por vapor.
P1 = 20308 / 0,3 = 67693 kilovatios,
o P1 = 67693 1.36 = 92062 hp. con
La potencia suministrada de la turbina en kcal / s está determinada por la fórmula Q = 0.24 · P · t;
Q t = 0,24 P = 0,24 67693 = 16246 kcal/seg.
13. Determine la sección transversal del cable de 22 m de largo a través del cual fluye la corriente hacia el motor trifásico de 5 litros. c) tensión 220 V al conectar el devanado del estator en triángulo cosfie= 0,8; · = 0,85. Caída de tensión admisible en los cables U = 5%.
Entrada de potencia al motor a potencia neta P2
P1 = (5 0,736) / 0,85 = 4,43 kW.
La corriente I = P1 / (U 1.73cosfie) = 4430 / (220 1.73 0.8) = 14.57 A.
En una línea trifásica, las corrientes se suman geométricamente, por lo que la caída de tensión en el conductor debe tomarse como U:1.73, no U:2 como para corriente monofásica. Entonces la resistencia del alambre:
r = (U: 1,73) / I = (11: 1,73) / 14,57 = 0,436 ohmios,
donde U está en voltios.
S = 1/57 22 / 0,436 = 0,886 mm2
La sección transversal de los cables en un circuito trifásico es menor que en un circuito monofásico.
14. Determine y compare las secciones transversales de los conductores para corrientes monofásicas y trifásicas directamente alternas. 210 lámparas de 60 W cada una para un voltaje de 220 V están conectadas a la red, ubicadas a una distancia de 200 m de la fuente de corriente. Caída de voltaje permitida 2%.
a) En corriente continua y alterna monofásica, es decir, cuando hay dos conductores, las secciones serán las mismas, porque bajo carga de iluminación cosfie= 1 y la potencia transmitida
P = 210 60 = 12600 W,
y la corriente I = P/U = 12600/220 = 57,3 A.
Caída de tensión admisible U = 220 2/100 = 4,4 V.
La resistencia de los dos cables es r = U / I 4.4 / 57.3 = 0.0768 Ohm.
Sección transversal del alambre
S1 = 1/57 * (200 * 2) / 0,0768 = 91,4 mm2.
Para la transferencia de energía, se requiere una sección transversal total de 2 S1 = 2 91,4 = 182,8 mm2 con una longitud de cable de 200 m.
b) Con corriente trifásica, las lámparas se pueden conectar en forma de triángulo, 70 lámparas por lado.
A cosfie= 1 potencia transmitida por los hilos P = 1,73·Ul·I.
I = P / (U 1.73) = 12600 / (220 1.73) = 33.1 A.
La caída de tensión admisible en un conductor de una red trifásica no es U · 2 (como en una red monofásica), sino U · 1,73. La resistencia de un cable en una red trifásica será:
r = (U: 1,73) / I = (4,4: 1,73) / 33,1 = 0,0769 ohmios;
S3ph = 1/57200 / 0,0769 = 45,7 mm2.
La sección transversal total de los hilos para una potencia de transmisión de 12,6 kW en una red trifásica con conexión en triángulo es menor que en una monofásica: 3 · S3ph = 137,1 mm2.
c) Cuando se conecta en estrella, se requiere una tensión de red U = 380 V para que la tensión de fase de las lámparas sea de 220 V, es decir, para que las lámparas se enciendan entre el hilo neutro y cada lineal.
La corriente en los cables será: I = P / (U: 1,73) = 12600 / (380: 1,73) = 19,15 A.
Resistencia del cable r = (U: 1,73) / I = (4,4: 1,73) / 19,15 = 0,1325 ohmios;
S3sv = 1/57200 / 0,1325 = 26,15 mm2.
La sección transversal total cuando se conecta en estrella es la más pequeña que se puede lograr aumentando el voltaje para transmitir una potencia dada: 3 · S3sv = 3 · 25,15 = 75,45 mm2.
Ver también: Cálculo de valores de fase y línea de corriente trifásica.