Cálculos para mejorar el factor de potencia en una red trifásica
 Al calcular la capacitancia de un capacitor para mejorar el factor de potencia en una red trifásica, seguiremos la misma secuencia que en el artículo. con ejemplos de cálculos en una red monofásica… El valor del factor de potencia está determinado por la fórmula de potencia para corriente trifásica:
Al calcular la capacitancia de un capacitor para mejorar el factor de potencia en una red trifásica, seguiremos la misma secuencia que en el artículo. con ejemplos de cálculos en una red monofásica… El valor del factor de potencia está determinado por la fórmula de potencia para corriente trifásica:
P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).
Ejemplos de
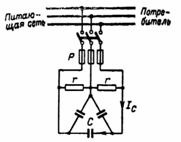
1. Un motor de inducción trifásico tiene los siguientes datos de panel: P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Conexión en estrella del estator. Supongamos que es difícil determinar el valor de cosφ del tablero y, por lo tanto, es necesario determinarlo. ¿A qué valor disminuirá la corriente después de mejorar el factor de potencia a cosφ = 1 usando capacitores? ¿Qué capacidad deben tener los condensadores? ¿Qué potencia reactiva compensarán los capacitores (Fig. 1)?
Las abrazaderas del devanado del estator están marcadas: inicio - C1, C2, C3, extremos - C4, C5, C6, respectivamente.Sin embargo, a continuación, para facilitar la comunicación con los diagramas, el origen se etiquetará como A, B, C y los extremos X, Y, Z.
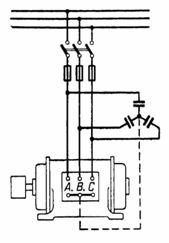
Arroz. 1.
Potencia motor P1 = P2 / η = 40000 / 0,85 ≈47000 W,
donde P2 es la potencia neta que se indica en la placa de identificación del motor.
cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.
Después de mejorar el factor de potencia a cosφ = 1, la potencia de entrada será:
P1 = √3 ∙ U ∙ ∙ 1
y la corriente caerá a
I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.
Esta es la corriente activa en cosφ = 0.69 ya que
Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.
En la Fig. 1 muestra la inclusión de capacitores para mejorar el cosφ.
Tensión del condensador Uph = U / √3 = 380 / √3 = 220 V.
La corriente de magnetización de fase es igual a la corriente de magnetización lineal: IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.
La resistencia capacitiva del condensador, que debe proporcionar la corriente de magnetización, será: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).
Por lo tanto, la capacitancia del capacitor C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79.8 / (220 ∙ 3.14 ∙ 100) = 79.800 / (22 ∙ 3.14) ∙ 10 ^ (- 6) = 1156.4 μF.
Se debe conectar un bloque de capacitores con una capacidad total de C = 3 ∙ 1156.4≈3469 μF a un motor trifásico para mejorar el factor de potencia a cosφ = 1 y al mismo tiempo reducir la corriente de 105 a 71.5 A.
La potencia reactiva total compensada por condensadores, que en ausencia de condensadores se toma de la red, Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.
En este caso, el motor consume potencia activa P1 = 47 kW solo de la red.
En la Fig.La figura 2 muestra un bloque de condensadores conectados en triángulo y conectados a los terminales de un motor trifásico cuyo devanado también está conectado en triángulo. Esta conexión de condensadores es más ventajosa que la conexión que se muestra en la fig. 1 (ver la conclusión del cálculo 2).
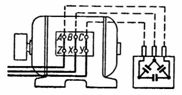
Arroz. 2.
2. Una pequeña central eléctrica alimenta una red trifásica con una corriente I = 250 A a una tensión de red U = 380 V y un factor de potencia de red cosφ = 0,8. La mejora del factor de potencia se consigue mediante condensadores que se conectan en triángulo según el diagrama de la fig. 3. Es necesario determinar el valor de la capacitancia de los capacitores y la potencia reactiva compensada.
Arroz. 3.
Potencia aparente S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.
Determine la potencia activa en cosφ = 0,8:
P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.
Potencia reactiva a compensar a cosφ = 0,8
Q = S ∙ senφ≈164,3 ∙ 0,6 = 98,6 kvar.
Por lo tanto, la corriente de magnetización lineal (Fig. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.
Corriente de fase magnetizante (capacitiva) ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.
La corriente del capacitor se puede determinar de otra manera por la corriente de magnetización (reactiva) en el circuito:
IL = I ∙ senφ = 250 ∙ 0,6 = 150 A,
ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.
Cuando se conectan en triángulo, cada grupo de capacitores tiene un voltaje de 380 V y una corriente de fase ICph = 86.7 A.
I = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.
Por lo tanto, C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.
La capacitancia total del banco de capacitores es C3 = 3 ∙ 726 = 2178 μF.
Los condensadores conectados permiten utilizar toda la potencia de la central eléctrica S = 164,3 kVA en forma de potencia neta.Sin condensadores de funcionamiento, solo se utiliza una potencia activa de 131,5 kW a cosφ = 0,8.
La potencia reactiva compensada Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 aumenta en proporción al cuadrado de la tensión. Por lo tanto, la capacidad requerida de los capacitores, y por lo tanto el costo de los capacitores, es menor porque el voltaje es mayor.
Las resistencias r en la fig. 3 se utilizan para descargar gradualmente los condensadores cuando se desconectan de la red.