Cálculo del elemento calefactor.

Para determinar uno de los parámetros principales del cable del elemento calefactor: diámetro d, m (mm), se utilizan dos métodos de cálculo: de acuerdo con la potencia de superficie específica admisible PF y utilizando la tabla de cargas actuales.

Potencia superficial específica admisible PF= P⁄F,

donde P es la potencia del calentador de alambre, W;

F = π ∙ d ∙ l — área del calentador, m2; l — longitud del cable, m.

Según el primer método

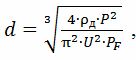
donde ρd — resistencia eléctrica del material del alambre a la temperatura real, Ohm • m; U es el voltaje del cable del calentador, V; PF: valores permisibles de potencia superficial específica para diferentes calentadores:

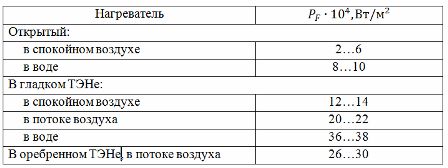
El segundo método utiliza una tabla de cargas actuales (consulte la Tabla 1) compilada a partir de datos experimentales. Para utilizar la tabla indicada, es necesario determinar la temperatura de calentamiento Tp calculada en relación con la temperatura real (o permitida) del conductor Td por la relación:

Tr = Km ∙ Ks ∙ Td,

donde Km es el factor de instalación, teniendo en cuenta el deterioro de las condiciones de refrigeración del calentador debido a su construcción; Kc es el factor ambiental, considerando la mejora de las condiciones de refrigeración del calentador en comparación con un entorno de aire estacionario.

Para un elemento calefactor de alambre retorcido en espiral, Km = 0,8 … 0,9; lo mismo, con base cerámica Km = 0,6 ... 0,7; para un cable de placas calefactoras y algunos elementos calefactores Km = 0,5 ... 0,6; para un conductor de un piso eléctrico, suelo y elementos calefactores Km = 0.3 ... 0.4. Un valor menor de Km corresponde a un calentador con un diámetro menor, un valor mayor a un diámetro mayor.

Cuando se opera en condiciones distintas a la convección libre, se toma Kc = 1.3 … 2.0 para los elementos de calentamiento en la corriente de aire; para elementos en agua tranquila Kc = 2,5; en el flujo de agua — Kc = 3,0 … 3,5.

Si se configuran el voltaje Uph y la potencia Pf del futuro calentador (diseñado), entonces su corriente (por fase)

Iph = Pph⁄Uph

De acuerdo con el valor calculado de la corriente del calentador para la temperatura calculada necesaria de su calentamiento de acuerdo con la tabla 1, se encuentra el diámetro requerido del alambre de nicromo d y la longitud requerida del alambre, m, para la fabricación del calentador es calculado:

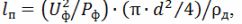
donde d es el diámetro del alambre seleccionado, m; ρd es la resistencia eléctrica específica del conductor a la temperatura de calentamiento real, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

donde αr - coeficiente de temperatura de resistencia, 1/OS.

Para determinar los parámetros de la espiral de nicromo, tome el diámetro promedio de las vueltas D = (6 … 10) ∙ d, el paso de la espiral h = (2 … 4) ∙ d,

número de vueltas

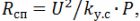
longitud de hélice lsp = h ∙ n.

Al calcular los elementos calefactores, debe recordarse que la resistencia del cable en espiral después de presionar el elemento calefactor

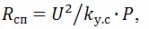
donde k (y.s) es un coeficiente que tiene en cuenta la reducción de la resistencia de la espiral; según datos experimentales, k (s) = 1,25. También debe tenerse en cuenta que la potencia superficial específica del alambre en espiral es 3,5 ... 5 veces mayor que la potencia superficial específica del elemento calefactor tubular.

En los cálculos prácticos del elemento calefactor, primero determine la temperatura de su superficie Tp = To + P ∙ Rt1,

donde Es la temperatura ambiente, °C; P es la potencia del elemento calefactor, W; RT1 — resistencia térmica en la tubería — interfaz media, ОC / W.

Luego se determina la temperatura del devanado: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

donde Rt2 es la resistencia térmica de la pared de la tubería, ОC / W; RT3 — resistencia térmica del relleno, ОC / W; Rp1 = 1⁄ (α ∙ F), donde α es el coeficiente de transferencia de calor, W / (m ^ 2 • ОС); F — área del calentador, m2; Rt2 = δ⁄ (λ ∙ F), donde δ es el espesor de la pared, m; λ — conductividad térmica de la pared, W / (m • ОС).

Para obtener más información sobre el dispositivo de los elementos calefactores, consulte aquí: Elementos de calentamiento. Dispositivo, selección, operación, conexión de elementos calefactores.

Tabla 1. Tabla de cargas actuales

Ejemplo 1. Calcule el calentador eléctrico en forma de espiral de alambre de acuerdo con la potencia superficial específica admisible PF.

Condición.Potencia del calentador P = 3,5 kW; tensión de alimentación U = 220 V; material del alambre — nichrome Х20Н80 (una aleación de 20% de cromo y 80% de níquel), por lo tanto, la resistencia eléctrica específica del alambre ρ20 = 1.1 ∙ 10 ^ ( — 6) Ohm • m; coeficiente de temperatura de resistencia αр = 16 ∙ 10 ^ (- 6) 1 /ОС; la espiral es abierta, en forma metálica, la temperatura de trabajo de la espiral es Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W/m2. Determine d, lp, D, h, n, lp.

Respuesta. Resistencia de la bobina: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohmios.

Resistencia eléctrica específica a Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Encuentre el diámetro del alambre:

De la expresión R = (ρ ∙ l) ⁄S obtenemos l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), de donde la longitud del cable

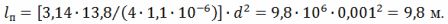
El diámetro promedio de la vuelta en espiral es D = 10 ∙ d = 10 ∙ 0.001 = 0.01 m = 10 mm. Paso de espiral h = 3 ∙ d = 3 ∙ 1 = 3 mm.

El número de vueltas de la espiral.

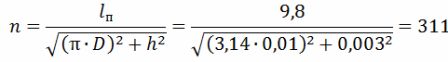
La longitud de la hélice es lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Ejemplo 2. Calcule estructuralmente el calentador de resistencia del cable al determinar el diámetro del cable d utilizando la tabla de cargas actuales (consulte la tabla 1).

Condición. Potencia del calentador de alambre P = 3146 W; tensión de alimentación U = 220 V; material de alambre — nicromo Х20Н80 ρ20 = 1.1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; hélice abierta ubicada en la corriente de aire (Km = 0.85, Kc = 2.0); temperatura de funcionamiento permitida del conductor Td = 470 ОС.

Determine el diámetro d y la longitud del alambre lp.

Respuesta.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

La corriente del calentador de diseño I = P⁄U = 3146⁄220 = 14,3 A.

De acuerdo con la tabla de cargas actuales (ver tabla 1) en Tr = 800 ОС e I = 14.3 A, encontramos el diámetro y la sección transversal del cable d = 1.0 mm y S = ​​0.785 mm2.

Longitud del cable lp = (R ∙ S) ⁄ρ800,

donde R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 ohmios, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = 1,11 ∙ 10 ^ (- 6) ohmios • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Además, si es necesario, de forma similar al primer ejemplo, se pueden definir D, h, n, lsp.

Ejemplo 3. Determinar el voltaje permisible del calentador eléctrico tubular (TEN).

Condición... La bobina del elemento calefactor está hecha de alambre de nicromo con un diámetro d = 0,28 mm y una longitud l = 4,7 m El elemento calefactor está en aire quieto con una temperatura de 20 °C. Características del nicromo: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. La longitud de la parte activa de la carcasa del elemento calefactor es La = 40 cm.

El elemento calefactor es liso, diámetro exterior dob = 16 mm. Coeficiente de transferencia de calor α = 40 W / (m ^ 2 ∙ ° C). Resistencias térmicas: relleno RT3 = 0,3 ОС / W, paredes de la carcasa Rт2 = 0,002 ОС / W.

Determine qué voltaje máximo se puede aplicar al elemento calefactor para que la temperatura de su bobina Tsp no exceda los 1000 ℃.

Respuesta. Temperatura del elemento calefactor del elemento calefactor

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

donde It es la temperatura del aire ambiente; P es la potencia del elemento calefactor, W; RT1: resistencia térmica de contacto de la interfaz tubería-medio.

Potencia del elemento calefactor P = U ^ 2⁄R,

donde R es la resistencia de la bobina de calentamiento.Por lo tanto, podemos escribir Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), de donde el voltaje en el elemento calefactor

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Encuentre R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

donde ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ∙ 10 ^ ( — 6) Ohm • m.

Entonces R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 ohmios.

Resistencia térmica de contacto RT1 = 1⁄ (α ∙ F),

donde F es el área de la parte activa de la carcasa del elemento calefactor; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Encuentre Rt1 = 1⁄ (40 ∙ 0.02 = 1.25) OC / W.

Determine el voltaje del elemento calefactor U = √ ((85.5 ∙ (1000-20)) / (1.25 + 0.002 + 0.3)) = 232.4 V.

Si la tensión nominal indicada en el elemento calefactor es de 220 V, entonces la sobretensión a Tsp = 1000 OS será del 5,6 % ∙ Un.